Académicamente y en la mayoría de ocasiones, el análisis de un proceso de compresión se realiza mediante análisis politrópico enfocado a gases ideales. Pero, ¿en qué desvío, respecto a la realidad, estamos incurriendo al usar gases ideales? 

En este artículo analizaremos las ecuaciones que nos permiten calcular y diseñar el proceso de compresión de gases ideales y reales, acorde a los estudios desarrollados y presentados por Jhon M. Schultz en 1962, aplicado a compresores centrífugos principalmente.

Este artículo explica con detalle el trabajo realizado por Schultz, mencionado anteriormente, y publicado por ASME en 1962.

A continuación encontrarás un índice, y si lo que buscas es ir directamente al paso a paso de cómo evaluar las variables de diseño de un comrpesor centrífugo real puedes ir a la sección 2.6. Pero si lo que quieres es dominar la termodinámica de la compresión, como el hombre que sentó las bases de su análisis moderno, te recomiendo una lectura completa.

Índice

1. Antes de empezar tienes que saber esto

1.1 ¿Qué es un proceso politrópico? 

1.1.1 ¿Qué es un análisis politrópico?

1.2 ¿Qué es un proceso isentrópico? 

2. Análisis del proceso de compresión

2.1 Análisis politrópico

2.2 Derivación de ecuaciones

2.3 Test de Evaluación

2.4 Análisis isentrópico

2.5 Factor de Trabajo Politrópico o "Polytropic Head Factor"

2.6 Diseño de Compresores

2.7 Presión Total y Temperatura

2.8 Flujo Lateral y refrigeración

2.9 Otras Aplicaciones

2.10 Funciones de Compresibilidad Genralizada

2.11 Ejemplo Numérico

3 Conclusiones y Recomendaciones

 

1. Antes de empezar tienes que saber esto

Antes de comenzar a analizar las relaciones matemáticas que nos permitirán despejar variables (o diseñar parámetros de proceso) de procesos de compresión, es conveniente que definamos ciertos conceptos sobre los que vamos a desarrollar todo el análisis.

1.1 ¿Qué es un proceso politrópico? 

Un proceso politrópico de compresión no es más que un proceso de compresión donde se cumple:

• P·V^n = cte.

Donde n es el exponete politrópico, el cual depende de muchos efectos reales: intercambio de calor con el entorno, irreversibilidades por fricción, etc... Para gases ideales y procesos adiabáticos reversibles, estamos acostumbrados a ver en la literatura general:

• n = gamma = Cp / Cv, lo que aplicaría solo a procesos politrópicos reversibles y adiabáticos (procesos ideales sin pérdidas, y sin intercambio de calor con el exterior).

Evaluar esta n, nos permitiría poder despejar muchas variables de un proceso de compresión, pero es una variable que para un proceso real, alberga una complejidad muy grande.

1.1.1 ¿Qué es un análisis politrópico?

Si quiesieramos evaluar un proceso que va desde el estado 1 al estado 2, aplicaríamos P·V^n = cte, para el estado 1 y 2, y despejaríamos las incógnitas. 

Pues bien, en un análisis politrópico evaluaríamos una parte finita de puntos entre los estados 1 y 2, para tener una foto más detallada del proceso. A esto se le conoce como análisis diferencial, que para el cálculo del trabajo si hacemos un análisis diferencial tendríamos por ejemplo:

• ΔW = V dP, donde tendríamos presente que PV^n = cte.

Esto es un ejemplo para ilustrar como el análisis diferencial nos permitirá calcular con mayor precisión procesos reales, las ecuaciones que intervendrán, las veremos más adelante.

1.2 ¿Qué es un proceso isentrópico? 

Es un proceso donde la entropía permanece constante durante el proceso. Esto quiere decir que el proceso es reversible y adiabático, es decir, es un proceso ideal sin pérdidas y además no hay intercambio de calor con el exterior.

Evaluar un proceso como si fuera isentrópico, nos permite evaluar las variables límite que la física de este proceso nos deja alcanzar (como podría ser la temperatura de descarga del compresor por ejemplo). De tal forma que podremos evaluar el rendimiento de un compresor dividiendo la enegría real consumida entre la energía isentrópica consumida.

2. Análisis del proceso de compresión

Enonces, ¿cómo podríamos pasar de un modelo de gases ideales a un modelo de gases reales? El principal parámetro que nos ayudará es el factor de compresibilidad "Z".

Z nos indica cuánto se desvía un gas real del comportamiento de un gas ideal en cuanto a su compresibilidad:

• Z = P·V / n·R·T
  • ​​​​​​Z = 1 → el gas se comprime como un gas ideal.
  • Z < 1 → el gas es más comprimible (las moléculas tienen menos fuerza de repulsión)
  • Z > 1 → el gas en menos comprimible (las moléculas tienen más fuerza de repulsión)

Pues bien, además de introducir al análisis politrópico el factor de compresibilidad Z, Schultz también introduce dos nuevas funciones: X e Y. Siendo estas funciones también sobre el fenómeno de compresibilidad, y pudiendo a partir de ellas caracterizar y graficar la compresibilidad de gases reales.

Schultz, en su estudio también desarrolla un análisis isentrópico, y al igual que para analizar el comportamiento de gases reales introduce Z, X e Y para el análisis politrópico, y para el análisis isentrópico en gases reales define el polytropic head factor, f, para ajustar el desvío entre el comportamiento ideal y real de los gases.

Introduzcámonos ahora en la descripción del proceso de compresión real, a partir del análisis politrópico realizado por Schultz.

2.1 Análisis politrópico

En esta sección Schultz define las ecuaciones que describen el proceso politrópico para un gas real, pero no pueden ser resueltas analíticamente por la complejidad de sus variables.

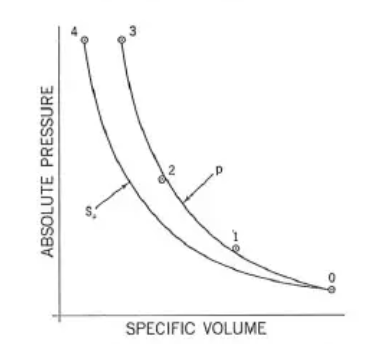
Este análisis se desarrolla entorno al hipotético test de un compresor centrífugo de 3 etapas, con lo que tendremos una descarga 1, 2 y 3, pero también una admisión, 0. Si tomaramos las muestras de presión y volumen en estos cuatro puntos en el gas comprimido (lo que llamaremos sistema), de este hipotético test, podríamos formar la curva mostrada en la figura 1.

Figura 1 Presión - Volumen diagrama del test de un compresor centrífugo [John M. Schultz, 1962]

Esta curva que llamaremos "p", dibujada entre los puntos 0 y 3, podría ser identificada como un proceso reversible descrito por el siguiente balance de energía:

• Qp + Wp = H3 - H0 (1)

Donde Qp es el calor reversible de entrada al sistema, y Wp es la energía neta de entrada. H representa entalpía.

Ahora si imagináramos que no hay intercambio de calor con el exterior, es decir, un proceso adiabático, podríamos describir el balance de energía de la siguiente manera:

• W = H3 - H0 + (v3 ^2 + v0 ^2) / 2·g (2)

Donde ahora identificamos con W la energía de entrada del eje y v la velocidad del gas. Esta ecuación 2 también puede ser escrita de la siguiente forma:

• W - ΔKE = H3 - H0  (2a)

Donde ΔKE es el incremento de energía cinética producida por el compresor.

Ahroa podemos relacionar el balance de energía en el gas desde el punto 0 al putno 3 uniendo las ecuaciones 1 y 2a de la siguiente forma:

• Qp + Wp = H3 - H0 → {Con la ecuación 2a sustituimos la diferencia de entalpía}

→ Qp + Wp = W - ΔKE (3)

Si todos los puntos de la curva fueran reversibles, y además adiabáticos (Qp = 0), la curva p coincidiría con la curva S0, ruta isentrópica que se puede ver en la figura 1.

Por lo tanto, podemos decir que Qp añade irreversibilidad o ineficiencia. Mientras que Wp es un valor de reversibilidad, que podemos usar para medir la máxima eficincia del proceso, es decir, la energía final del sistema partido de la energía de entrada al sistema:

• e = Wp / (H3 - H0) = Wp / (W - ΔKE) (4)

Donde e es la eficiencia del compresor de la curva "p", proceso politrópico reversible.

Vamos a diseccionar un poco más esta ecuación 4, descomponiendo Wp:

• Wp = ∫ V·dP (5)

Con la evaluación de la integral entre los límites de P3 y P0 y donde V es volumen especifico (no volumen).

Es importante aquí observar que describir el trabajo en un compresor centrífugo (como es este caso) es diferente de un compresor recirpocante de pistón:

• Centrífugo, flujo constante Wp = ∫ V·dP
• Reciprocante, flujo alternativo Wp = ∫ P·dV

Entonces como decíamos, podemos describir la ecuación 4 ahora como:

• e = Wp / (H3 - H0) →

→ e = ∫ V·dP / (H3 - H0) (4a)

Como podemos apreciar, esta eficiencia esta acotada entre los puntos 3 y 0, pero ¿sería igual entre 1 y 0, entre 2 y 1 y entre 3 y 2? incluso, ¿sería igual para cualquier diferencial de esta curva? La respuesta es que sí, y esto se puede justificar matemáticamente con la siguiente expresión:

• e = ∫ V·dP / (H3 - H0) → 

e ≈ V·(dP / dH) (6)

Esta expresión nos dice que para dos puntos cualquiera de la curva "p", el incremento de presión entre el imcremento de entalpía entre dos puntos, multiplicado por el volumen específico, da siempre una constante, la cual llamamos eficiencia (e). Pero podemos notar que e no es igual, si no aproximado, veamos por qué. Para poder transformar la ecuación 4a a la ecuación 6, solo tenemos que usar una "artimaña" matemática:

• Tenemos ∫ V·dP → {añadimos un factor dH/dH} → ∫ V·(dH/dH)·dP, entonces cambiamos la derivada de integración de dP a dH, resultando en el siguiente efecto:
  • Cambio de integración: dP = (dP / dH)·dH → 

e = ∫ V·dP / (H3 - H0) = [1/(H3 - H0)]·∫ V(H)·(dP/dH)(H)·dH, para los límites de la integral de H0 y H3 ahora, en lugar de P0 y P3.

Aplicando una primera aproximación para extraer V de la integral ...

Si asumimos que recorrido de la curva politrópica infinitesimal, muy pequeño, V(H) apenas varía entre los dos puntos de los límites de la integral, entonces tenemos:

e ≈ [Vmedio/(H3 - H0)]·∫(dP/dH)·dH, y ahora la integral se resuelve como ...

∫(dP/dH)·dH = ∫(d/dH)·P(H)·dH = P(H3) - P(H0) = P3 - P0, si juntamos todo finalmente ...

e ≈ [Vmedio/(H3 - H0)]·(P3 - P0) → y ahora en la curva "p", si cogemos dos puntos infinitesimales y asumimeos que el tramo es lineal, podemos aproximar y decir que:

e ≈ V·(dP / dH)

Muy bien, entonces hemos desarrollado el balance de energía de la curva "p" (ecuación 3), y la eficiencia (ecuación 4) como una constante que se da para cualquier par de puntos de esta misma curva.

Recordemos también que la curva "p" debería coincidir con la curva S0 (isentrópica), si estimamos Qp = 0. Si expresemos el balance de energía general de la ecuación 1 en diferencial (para amplitudes infinitesimales):

• (ec. 1) → H3 - H0 = Wp + Qp → 

​​​​​​→ ​dH = V·dP + T·dS (7)

Donde la anterior expresión diferencial, si la hacemos para un proceso isentrópico (dS = 0) nos dejaría una forma como:

• dH = V·dP + 0 → 1 = V·(dP/dH) + 0

→ 1 = V·(dP/dH) (8)

Con lo que resumiendo, la ecuación 6, eficiencia de un proceso politrópico (e = V·(dP / dH)), se puede ajustar a la curva de un proceso isentrópico bajo las siguientes premisas que hemos tratado anteriromente:

• Qp = 0
• Wp = W - ΔKE
• e = 1

Nos dirigiremos a estas expresiones como a la relación (9).

Como hemos visto anteriormente, la ecuación 6 es una aproximación (e ≈ V·(dP / dH)) debido a que V es una función que para un gas real resulta compleja, por depender de varias funciones V = f (P, H, T, ...). Con lo que no es posible resolver directamente  Wp = ∫ V·dP, ya que para ello V solo debería depender de P, V(P). Y cuando hacemos el cambio de variable para obtener ∫ V(H)·(dP/dH)(H)·dH, tenemos que suponer que V(H) no es conocido, y por ello aproximamos que V es constante. Este bloqueo matemático, que nos impide resolver analíticamente las descripciones matemáticas de un proceso politrópico real, llevan a Schultz a buscar una integración numérica, para aproximar la solución real mediante un proceso iterativo.

¿Es posible reorganizar las anteriores ecuaciones para poder integrar directamente ∫ V·dP en la ecución e = ∫ V·dP / (H3 - H0)?

2.2 Derivación de ecuaciones

En esta seccción veremos como Schultz llega a una expresión de Wp que finalmente puede ser resuelta. Recordemos qué variables están involucradas en esta expresión (ecuación 4a):  e = ∫ V·dP / (H3 - H0) → Volumen específico, entalpía y dP.

Empecemos por diseccionar la función entalpía, para cualquier gas homogeneo esta puede ser repesentada como una función de la presión y de la temperatura en dos formas:

• Forma 1:
  • (dH / dP) = (∂H/∂P)T + (∂H/∂T)P · (dT/dP), Schultz obtiene esto aplicando la "regla de la cadena multivariable", aplicada cuando H = H (T, P). Su publicación no incluye el desarrollo.
• Forma 2:
  • (∂H/∂P)T · (∂P/∂T)H · (∂T/∂H)P = -1, Schultz obtiene esta forma de un resultado general de cálculo diferencial, llamado "identidad cíclica de derivadas parciales" {(∂x/∂y)z + (∂y/∂z)x (∂z/∂x)y = -1}, aplicado a las variables de la forma 1 (H, P, T). Su publicación no incluye el desarrollo.

Nos referiremos a estas dos ecuaciones como (10).

Algunas derivadas vistas en la relación 10, pueden ser simplificadas por expresiones como el coeficiente de Joule-Thompson o el calor específico a presión constante, siendo estas expresiones:

• Coeficiente de Joule-Thompson → JT = (∂T/∂P)H, definición termodinámica del proceso de Joule-Thompson.
• Calor específico a presión constante →  Cp = (∂H/∂​T​​​​​)P, definición fundamental que proviene del primer principio de la termodinámica aplicada a un sistema cerrado con trabajo de frntera P·dV.

Nos referiremos a estas expresiones como (11).

Con lo que sustituyendo en 10, tenemos:

• (dH / dP) = (∂H/∂P)T + (∂H/∂T)P · (dT/dP) → {Cp = (∂H/∂​T​​​​​)P} → (dH / dP) = (∂H/∂P)T + Cp · (dT/dP)

Ahora nos quedaría por sustituir el término (∂H/∂P)T, que podríamos obtenerlo con la forma 2 de la relación 10:

Forma 2 de relación 10 → (∂H/∂P)T · (∂P/∂T)H · (∂T/∂H)P = -1 → (∂H/∂P)T = (1 / (∂P/∂T)H) · (1 / (∂T/∂H)P) · (-1) donde:

• (1 / (∂P/∂T)H) = (∂T/∂P)H = JT
• (1 / (∂T/∂H)P) = (∂H/∂​T​​​​​)P = Cp

Reemplazando... (∂H/∂P)T = (1 / (∂P/∂T)H) · (1 / (∂T/∂H)P) · (-1) → (∂H/∂P)T = - JT · Cp

Y ahora reemplazando esta expresión anterior en la forma 1, la cual habíamos empezado ...

(dH / dP) = (∂H/∂P)T + Cp · (dT/dP) → (dH / dP) = - JT · Cp + Cp · (dT/dP) →

(dH / dP) = Cp · ((dT/dP) - JT) (10a)

Bien, diseccionando la funicón de entalpia hemos llegado hasta esta relación de 10a, pero aún podemos reemplazar más términos de esta expresión. Definamos un poco más el coeficiente de JT, con este objetivo de seguir desarrollando la función de entalpía. Otra relación termodinámica para gases homogéneos es:

• JT = [T · (∂V/∂T​​​​​​)P - V] / Cp  (12), proviene de combinar 3 relaciones:
  • La identidad termodinámica: dH = V·dP + T·dS
  • La ecuación de Maxwell: (∂S/∂P)T = (∂V/∂​T)P
  • La definición del coeficiente de Joule-Thompson que hemos visto:  JT = (∂T/∂P)H

La publicación de Schultz no incluye el desarrollo de estas tres ecuaciones para llegar a ecuación 12.

En esta expresión (12) encontramos la derivada de la función volumen específico respecto de la temperatura a presión constante. Volumen específico, otra de las funciones que hemos comentado en el inicio de esta sección 2.2, que tenemos como objetivo desarrollar para poder encontrar solución a Wp. Una forma de desarrollar la función volumen es la ecuación general de estado para cualquier gas:

• P·V = Z·R·T (13), donde Z es el factor de compresibilidad y R la constante individual del gas tratado (no confundir con la constante de los gases idelaes Ru = 8,314 kJ/mol·K. Recordar que R es Ru / M, donde M es la masa molar del gas tratado).

Si derivamos el volumen específico respecto de la temperatura en la ecuación 13, podemos obtener la siguiente expresión:

• P·V = Z·R·T → V = (Z·R·T)/T → V = (R / P)·Z·T → {Aplicamos la regla del producto para transformar Z(T)·T}

 → (∂V/∂T​​​​​​)P = (R/P)·[Z + T·(∂Z/∂T​​​​​​)P] y para expresar la función en V, Z y T usamos la relación ...

 P·V = Z·R·T → R / P = V / (Z·T) → (∂V/∂T​​​​​​)P = [V / (Z·T)]·[Z + T·(∂Z/∂T​​​​​​)P] y para acabar factorizando Z ...

(∂V/∂T​​​​​​)P = (V/T)·[1 + (T/Z)·(∂Z/∂T​​​​​​)P] (14)

Esta expresión es muy útil para expresar cómo varía el volumen específico con la temperatura. Y usándola ahora para combinarla en la ecuación 12, tenemos:

• JT = [T · (∂V/∂T​​​​​​)P - V] / Cp → {sustituyendo: (∂V/∂T​​​​​​)P = (V/T)·[1 + (T/Z)·(∂Z/∂T​​​​​​)P]}

JT = (V / Cp) · (T / Z) · (∂Z/∂T​​​​​​)P (12a) 

Bien, recordemos que hemos empezado desarrollando la expresión diferencial de la entalpía, donde llegamos a una expresión final como la ecuación 10a. Y en ese punto estabamos ahondando en la sustitución del coeficiente de Joule-Thompson por su expresión diferencial, pues aquí lo tenemos sustituyendo en la ecuación 10a la reciente ecuación 12a:

• (dH / dP) = Cp · ((dT/dP) - JT) → {sustituyendo JT por la ecuación 12a} → 

(dH / dP) = Cp · ((dT/dP) - V · (T / Z) · (∂Z/∂T​​​​​​)P) (10b)

Y ahora vamos iluminando un poco más nuestro propósito inicial, reconstruir la expresión 6 para permitir la integración directa de 5 en la expresión 4a. Vamos entonces a sustituir la expresión de la derivada de la entalpía respecto de la presión (ecuación 10b), y la expresión 13, ambas en la ecuación 6:

• (6) e = V·(dP / dH) → {sustituimos (10b) (dH / dP) = Cp · ((dT/dP) - V · (T / Z) · (∂Z/∂T​​​​​​)P)} →

e = V · Cp · ((dT/dP) - V · (T / Z) · (∂Z/∂T​​​​​​)P) → {sustituimos (13) V = (Z·R·T) / P} →

e = [(Z·R·T) / P] · Cp · ((dT/dP) - V · (T / Z) · (∂Z/∂T​​​​​​)P), reordenando la expresión ...

(P / T) · (dT / dP) = (Z·R / Cp) · [(1 / e) + (T / Z) · (∂Z/∂T​​​​​​)P] (6a)

Además de las ecuaciones de la relación 10, otra relación general termonidnámica para cualquier gas homogeneo es:

• Cp - Cv = T · (∂P/∂T​​​​​​)V · (∂V/∂T​​​​​​)P (15), donde Cv es el calor esoecífico a volumen constante. Esta expresión proviene de 3 principios básicos de la termodinámica:
  • Las identidades fundamentales:
    • dH = V·dP + T·dS
    • dU = T·dS + P·dV
  • Las definiciones de capacidades caloríficas:
    • Cv = (∂U/∂T​​​​​​)V ; Cp = (∂H/∂T​​​​​​)P
  • La ecuación de Maxwell:
    • (∂S/∂V​​​​​​)T = (∂P/∂T​​​​​​)V 

Schhultz no desarrolla en su publicación como llegar desde estas relaciones a la expresión 15.

Podemos describir el calor específico a volumen constante de la siguiente manera:

• Cv = (∂E/∂T​​​​​​)P (16), donde E es la energía interna.

Tenemos que notar que en la expresión 15, Schultz busca desarrollar la derivada de la presión respecto de la temperatura, (∂P/∂T​​​​​​)V. Recordemos que la expresión que Schultz busca resolver es e = ∫ V·dP / (H3 - H0), donde teníamos las variables V, H y dP. En la relación 10 hemos intentado desarrollar la función H, en la relación 13 hemos intentado desarrollar la función V, y ahora con la relación 15 intentaremos desarrollar dP. Para buscar una expresión de dP, al igual que para hacerlo con V usamos la ecuación 13, aquí volvemos a hacer lo mismo:

• (13) P·V = Z·R·T → P = (Z·R·T)/V → P = (R / V)·Z·T → {Aplicamos la regla del producto para transformar

Z(T)·T → (∂P/∂T​​​​​​)V = (R/V)·[Z + T·(∂Z/∂T​​​​​​)P] y para expresar la función en P, Z y T usamos la relación ...

P·V = Z·R·T → R / V = P / (Z·T) → (∂P/∂T​​​​​​)V = [P / (Z·T)] · [Z + T·(∂Z/∂T​​​​​​)P] y para acabar factorizando Z ...

(∂P/∂T​​​​​​)V = (P/T) · [1 + (T/Z)·(∂Z/∂T​​​​​​)V] (17), esto es el mismo proceso que hemos seguido para la ecuación 14 con el volumen específico.

Asi que ahora que hemos desarrollado la derivada de la presión respecto a la temperatura, la sustituimos en la ecuación 15, al igual que la ya conocida derivada del volumen específico respecto a la temperatura:

• (15) Cp - Cv = T · (∂P/∂T​​​​​​)V · (∂V/∂T​​​​​​)P → sustituyendo con las ecuaciones 17 y 14 ...

Cp - Cv = Z · R · [1 + (T/Z)·(∂Z/∂T​​​​​​)V] · [1 + (T/Z)·(∂Z/∂T​​​​​​)P] (15a)

Si ahora sustituimos esta expresión evaluada para Z·R en la ecuación 6a, desarrollaríamos la siguiente expresión:

• (15) Cp - Cv = Z · R · [1 + (T/Z)·(∂Z/∂T​​​​​​)V] · [1 + (T/Z)·(∂Z/∂T​​​​​​)P] → Z · R = ...

Z · R = (Cp - Cv) / [1 + (T/Z)·(∂Z/∂T​​​​​​)V] · [1 + (T/Z)·(∂Z/∂T​​​​​​)P], sustituyendo esto en 6a ahora ...

(6a ) (P / T) · (dT / dP) = (Z·R / Cp) · [(1 / e) + (T / Z) · (∂Z/∂T​​​​​​)P] → reemplazamos ...

(P / T) · (dT / dP) = [ [(k -1)/k] + [(1/e) + (T/Z)·(∂Z/∂T​​​​​​)P] ] / [1 + (T/Z)·(∂Z/∂T​​​​​​)V] + [1 + (T/Z)·(∂Z/∂T​​​​​​)P ] (6b)

Donde para la anterior expresión 6b hemos introducido un nuevo parámetro, que Schultz reconoce como el ratio de calor específico k, el cual usamos para simplificar la siguiente expresión:

• k = Cp / Cv (18)

Con esta ecuación 6b, Schultz muestra desarrollada la expresión dP, explícitamente como dT/dP. 

Entonces comenzábamos esta sección intentando desarrollar las funciones H, V y dP. Ya hemos visto el desarrollo de estas tres, pero para V simplemente la habíamos dejado expresada de forma general a partir de la ecuación 13, y también su variación respecto a la variación de la temperatura (∂V/∂T​​​​​​)P, donde esto último aparece en expresiones como la ecuación 15.

Pues bien, nos faltaría discutir el desarrollo de la relación de la variación del volumen específico con respecto a la variación de la presión (∂V/∂P​​​​​​)T. Para buscar este desarrllo, Schultz se apoya en otra expresión para cualquier gas homogéneo donde V aparece como una función de P y de T:

• (dV / dP) = (∂V/∂P)T + (∂V/∂T)P · (dT/dP) (19), Schultz obtiene esto aplicando la "regla de la cadena", aplicada a una función de dos variables, en este caso V = V (P, T). Su publicación no incluye el desarrollo para llegar a la ecuación 19.
• (∂V/∂P)T · (∂P/∂T)V · (∂T/∂V)P = -1 (20), Schultz obtiene esta forma de un resultado general de cálculo diferencial, llamado "identidad cíclica de derivadas parciales" {(∂x/∂y)z + (∂y/∂z)x (∂z/∂x)y = -1}, aplicado a las tres variables presentes V, P y T. Su publicación no incluye el desarrollo para llegar a la ecuación 19.

Entonces vayamos desgranando cada una de estas derivadas del volumen específico. La primera derivada del volumen que podemos desarrollar es (∂V/∂P)T, y esto podemos hacerlo reodenando la ecuación 13 como hemos hecho ya en otras ocasiones:

• (13) P·V = Z·R·T → V = (Z·R·T)/P → {Derivamos respecto de P a T constante, con lo que RT es constante}

(∂V/∂P​​​​​​)T = (R·T)·(∂/∂P)·(Z/P)T  = (R·T)·(P·(∂Z/∂P​​​​​​)T - Z)/P^2 {La derivada de Z/P respecto de P, es -Z/P^2}, ahora sustituyendo R·T por los términos V, P y Z ...

P·V = Z·R·T → R·T / P = V / Z· → (∂P/∂T​​​​​​)V = (V / Z) · [(∂Z/∂P​​​​​​)P - (Z/P)] y esarrollando y factorizando V / P ...

(∂V/∂P​​​​​​)T = - (V/P) · [1 - (P/Z)·(∂Z/∂P​​​​​​)T] (21), esto es el mismo proceso que hemos seguido para la ecuación 14 con el volumen respecto del tiempo.

Volvamos a la ecuación 19, donde teníamos las derivadas del volumen específico respecto de la temperatura y respecto de la presión. Ahora estas derivadas pueden ser sustituidas por los desarrollos que hemos ido haciendo:

• (∂V/∂P)T → Desarrollado en la ecuación 21
• (∂V/∂T)P → Desarrollado en la ecuación 14

Con lo que nos quedaríamos con la siguiente expresión ...

(P/V)·(dV/dP) = - [1 - (P/Z)·(∂Z/∂P)T] + [1+ (T/Z)·(∂Z/∂T)P] (P/T)·(dT/dP) (6c)

Donde la expresión (P/T)·(dT/dP) ha sido desarrollada tanto en la ecuación 6a como en la 6b. Por otro lado, al igual que en la ecuación 19 hemos sustituido las expresiones diferenciales del volumen, podemos también para la ecuación 20 hacer las siguientes sustituciones:

• (∂V/∂P)T → Desarrollado en la ecuación 21.
• (∂P/∂T)V → Desarrllado en la ecuación 17.
• (∂T/∂V)P → Desarrollado en la ecuación 14, a la inversa.

Con lo que nos quedaría la siguiente expresión ...

[1 - (P/Z)·(∂Z/∂P)T] = [1+ (T/Z)·(∂Z/∂T)P] / [1+ (T/Z)·(∂Z/∂T)V] (20a)

Si ahora sustituimos en en 6c las siguientes expresiones:

• (P/T)·(dT/dP) → Desarrollado en en 6b.
• [1 - (P/Z)·(∂Z/∂P)T] → Desarrollado en 20a.

Sustituyendo ...

(P/V)·(dV/dP) = ([(1/e)-1] - (1/k)·[(1/e) + (T/Z)·(∂Z/∂T)P]) / [1+ (T/Z)·(∂Z/∂T)V] (6d)

Finalmente, la ecuación 13 podría ser escrita de la siguiente forma aplicándole una diferenciación:

• Partimos de P·V = Z·R·T, y diferecniamos totalmente respecto de P. Tratando V, T y Z como funciones de P, donde R es constante:
  • Diferenciación del lado izquierdo de la ecuación, P·V → (d/dP)·(P·V) = P·(dV/dP) + V
  • Diferenciación del lado derecho de la ecuación, Z·R·T → (d/dP)·(Z·R·T) = R·(Z·(dT/dP) + T·(dZ/dP))
  • Igualando ambas expresiones → P·(dV/dP) + V = R·(Z·(dT/dP) + T·(dZ/dP))
  • Añadimos (1/R·T) para introducir V y P usando la ecuación de estado cuando haga falta: [P·(dV/dP) + V] / R·T = Z·(1/T)·(dT/dP) + (dZ/dP)
  • Sustituimos 1/(R·T) = Z/(P·V) → Z·[(1/V)·(dV/dP) + (1/P)] = Z·(1/T)·(dT/dP) + (dZ/dP) → dZ/dP = Z·((1/V)·(dV/dP) + (1/P) - (1/T)·(dT/dP))
  • Multiplicamos por P/Z a ambos lados y ...

(P/Z)·(dZ/dP) = 1 - (P/T)·(dT/dP) + (P/V)·(dV/dP) (6e)

Tenemos por tanto una expresión diferencial de la ecuación general de estado para cualquier gas, donde podemos observar que hemos desarrollado a lo largo de esta sección la siguientes expresiones:

• (P/T)·(dT/dP) → en la ecuación 6a y 6b también.
• (P/V)·(dV/dP) → en la ecuación 6d y 6c también.
• (P/Z)·(dZ/dP) → en la ecuación 6e.

Con lo que hasta el punto actual hemos descrito con varios desarrollos la ecuación 6 (e ~ V·(dP / dH)), cada uno de estos desarrollos determina la trayectoria de la curva "p" para una eficiencia constante e. Recordemos que esta curva "p" viene siendo la curva de presión respecto al volumen del hipotético test de un compresor centrífugo de estapas 0, 1, 2, 3, base del análsis de Schultz. Entonces, estos desarrollos de la ecuación 6 pueden resumirse de la siguiente forma:

• (P/T)·(dT/dP) = m → llamado exponente politrópico de temperatura, describiendo entonces esta relación diferencial a lo largo de "p".
• (P/V)·(dV/dP) = - (1/n) → n, exponente politrópico de volumen específico, describiendo esta relación diferencial del volumen específico a lo largo de "p".
• (P/Z)·(dZ/dP) = [(n-1)/n] - m 

Nos referiremos de aquí en adelante a este conjunto de relaciones como (6f).

Las diferentes relaciones diferenciales de los desarrollo de la ecuación 6, son resumidos en estas variables creadas por Schultz, ya que son expresiones diferenciales que aparecerán en sucesivos desarrollos, y permitirán trabajar de forma más resumida. Donde las variables "m" y "n" son desarrolladas por Schultz de la siguiente forma, en base a los desarrollos diferenciales de la ecuación 6 tratados anteriormente:

• m = (Z·R / Cp) · [(1/e) + X] = [((k - 1) / k) · ((1/e) + X)] / [L · (1 + X)]
• n = 1 / (Y - m · (1 + X)) = L / [(1 / k) · ((1/e) + X) - ((1/e) - 1)]

Nos referiremos de aquí en adelante a este conjunto de relaciones como (6g).

Observamos para las relaciones de 6g, cómo aparecen nuevas variables que encapsulan relaciones diferenciales y otras expresiones desarrolladas en las distintas expresiones de la ecuación 6, las cuales han sido desarrolladas en las diferentes expresiones de 6 (6a, 6b, etc...). El desarrollo de estas nuevas variables es por tanto:

• X = (T/Z)·(∂Z/∂T)P = (T/V)·(∂V/∂T)P - 1, donde X es definida por Schultz como función de compresibilidad.
• Y = 1 - (P/Z)·(∂Z/∂P)T = - (P/V)·(∂V/∂P)T, donde Y es definida por Schultz como función de compresibilidad.
• L = 1 + (T/Z)·(∂Z/∂T)V = (T/P)·(∂P/∂T)V, donde L es definida por Schultz como función de compresibilidad.

Nos referiremos de aquí en adelante a este conjunto de relaciones como (22).

Pero, ¿las tres se llaman igual? Sí, Schultz las denomina igual ya que las tres son efectivamente funciones de compresibilidad, donde cada una de ellas nos habla del comportamiento del factor de compresibilidad respecto a la variación de la temperatura y la presión.

Tomando estas expresiones de la relación 22, y sustituyendo en la ecuación 12a, 15a y 20a tenemos:

• (12a) JT = (V / Cp) · (T / Z) · (∂Z/∂T​​​​​​)P → sustituyendo por X tenemos ...

JT = (V / Cp) · X (12b)

• (15a) Cp - Cv = Z · R · [1 + (T/Z)·(∂Z/∂T​​​​​​)V] · [1 + (T/Z)·(∂Z/∂T​​​​​​)P] → sustituyendo por L y X tenemos ...

 Cp - Cv = Z · R · L (1 + X) (15b)

• 20a) [1 - (P/Z)·(∂Z/∂P)T] = [1+ (T/Z)·(∂Z/∂T)P] / [1+ (T/Z)·(∂Z/∂T)V] → sustituyendo por Y, X y L tenemos ...

L = (1 + X) / Y (20b)

Observando la ecuación 20b, podemos ver que podríamos expresar L en función de X y de Y, para facilitar el desarrollo de las expresiones. Por ejemplo, en nuestro enfásis por desarrollar la ecuación 6, que a estas alturas de artículo ya hemos llegado a la forma 6g, vamos a reemplazar L por  esta expresión:

• para m → m = (Z·R / Cp) · [(1/e) + X] = [((k - 1) / k) · ((1/e) + X) · Y] / (1 + X)^2
• para n → n = 1 / (Y - m · (1 + X)) = (1 + X) / [Y · [(1 / k) · ((1/e) + X) - ((1/e) - 1)]]

Nos referiremos de aquí en adelante a este conjunto de relaciones como (6h).

Y para el caso de la ecuación 15b, sustituyendo L tendríamso también:

• Cp - Cv = Z · R · [(1 + X)^2] / Y (15c)

LLegados a este punto, vamos a comparar estos desarrollos diferenciales de un proceso politrópico para gases reales, respecto a las expresiones bajo condiciones ideales.

Caso ideal - proceso isentrópico

Empezando por describir la curva "p" como la curva isentrópica, recordemos que la diferencia entre ambas es que e = 1, esto daría lugar a modificar las relaciones de 6h a:

• para m → ms = (Z·R / Cp) · (1 + X) = [(k - 1) / k] · [Y / (1 + X)], donde dnotamos con S para ms un proceso con entropía constante.
• para n → ns = 1 / [Y - ms · (1 + X)] = k / Y

Nos referiremos de aquí en adelante a este conjunto de relaciones como (6i).

Y esta relación anterior para ns a la que hemos llegado tras el desarrollo diferencial, puede ser avalado por la relación termodinámica general para cualquier gas homogéneo:

• (∂V/∂P)S = (1 / k) · (∂V/∂P)T (23), Schultz saca esta expresión de la definición del exponente iséntrópico k.

Esta realción 23 podría ser reescrita a través de 6f y 22 de la siguiente forma:

• P / V · (∂V/∂P)S = - 1/ns = - Y / k (23a), que es la misma expresión a la que se llega en la realción 6i para ns.

Caso ideal - proceso isentálpico (adiabático y reversible)

Otro caso especial, además del proceso isentrópico, es un proceso a entalpía constante (isentálpico), donde la eficiencia tiende a infinito (e → ∞). En este caso las relaciones 6h se quedarían con el siguiente aspecto:

• para m → mH = (Z·R / Cp) · X = [(k - 1) / k] · [(X · Y )/ (1 + X)^2], donde dnotamos con H para mH un proceso con entalpía constante.
• para n → nH = 1 / [Y - mH · (1 + X)] = (1 + X) / [Y · (1+(X/k))]

Nos referiremos de aquí en adelante a este conjunto de relaciones como (6j).

Caso ideal - proceso a presión constante (isobaro)

Otro caso ideal, un proceso a presión constante, para el que e = 0. Con lo que expresaríamos 6h como:

• para m → mP = ∞, donde denotamos con P para mP un proceso con entalpía constante.
• para n → nP = 0

Nos referiremos de aquí en adelante a este conjunto de relaciones como (6k).

Caso ideal - proceso con un volumen específico constante (isocoro)

Para un proceso a volumen específico constante, desde los desarrollos de las relaciones 6c, 6f y 22 podemos desarrollar las siguientes relaciones para m y n:

• para m → mV = Y / (1 + X), donde denotamos con V para mV un proceso con volumen específico constante.
• para n → nV = ∞

Nos referiremos de aquí en adelante a este conjunto de relaciones como (24).

Caso ideal - proceso con una temperatura constante (isotermo)

Para un proceso a temperatura constante, desde los desarrollos de las relaciones 6c, 6f y 22, nuevamente, podemos desarrollar las siguientes relaciones para m y n:

• para m → mT = 0, donde denotamos con T para mT un proceso con temperatura constante.
• para n → nT = 1 / Y

Nos referiremos de aquí en adelante a este conjunto de relaciones como (25).

Caso ideal - proceso con gas ideal

Bien, pues a todos estos casos anteriores que recogen varias procesos ideales, podemos considerar otro caso, el de un gas ideal. Para el caso de un gas ideal las funciones de compresibilidad descritas tienen la siguiente forma: X = 0, Y = Z = 1. Con lo que las variables desarrolladas en esta sección podrían describirse de la siguiente forma, a través de esta descripción de las funciones de compresibilidad par un gas ideal:

• m' = (k - 1) / kc = (n' - 1) / n'
• ms' = (k - 1) / k
• ns' = k
• mH' = mT' = 0 
• nH' = nT' = 1

Nos referiremos de aquí en adelante a este conjunto de relaciones como (6l).

Las expresiones de n, para estas relaciones de 6l, son las típicas ecuaciones que vemos en todas las bibliografías de termodinámica para describir un proceso politrópico para gases ideales. Puedes comparar esto con este **artículo** donde se explica el proceso politrópico para gases ideales.

Y con el resto de variables desarrolladas en esta sección, para gas ideal ahora:

• mV' = 1 (24a)
• JT' = 0 (12c)
• Cp'- Cv' = R (15d)

Donde para todas estas expresiones, denotamos con el símbolo ' un gas ideal. Shultz muestra estas relaciones para gases ideales y distintas condiciones ideales, ya que resulta interesante compararlas con las expresiones en condiciones de gas real para un proceso politrópico.

Volviendo a la ecuación 6f podemos ver que ninguno de los desarrollos de las relaciones que salen de la ecuación 6 nos permiten una integración directa de la ecuación 5, objeto de esta sección, ya que tanto m como n son variables. Pero Schultz sospecha que estas variables son relativamente constantes en comparación a P, V y T. Si esta consideración como constantes fuera tomada así, la integración de 6f tendría el siguiente resultado:

• (P/T)·(dT/dP) = m → integrando con m como una constante ...

(1/T)·dT = m·(1/P)·dP → ∫(1/T)·dT = m·∫(1/P)·dP → Ln(T) = m·Ln(P) + C → Si eliminamos los neperianos por simplificar la expresión ... → Ln(T) - m·Ln(P) = C → Ln(T / P^m) = C → (T / P^m) = e^C → (P^m / T) = (1 / e^C)

{notar que e^C sigue siendo una constante, y que la inversa de una constante también sigue siendo una constante}

P^m / T = constante

• (P/V)·(dV/dP) = - (1/n) → integrando con n como una constante ...

(1/V)·dV = -(1/n)·(1/P)·dP → ∫(1/V)·dV = -(1/n)·∫(1/P)·dP → Ln(V) = -(1/n)·Ln(P) + C →

Ln(V) + Ln[P^(1/n)] = C → Ln(V · [P^(1/n)]) = + C → V·P^(1/n) = e^C → buscando una forma similar a la ecuación de proceso politrópico, elevamos todo a n ... → [V·P^(1/n)]^n = e^(C·n) ... 

​​​​​P·V^n = constante

• (P/Z)·(dZ/dP) = [(n-1)/n] - m → integrando con n y m como dos constantes ...

(1/Z)·dZ = a·(1/P)·dP → {Donde a = [(n-1)/n] - m} → ∫(1/Z)·dZ = a·∫(1/P)·dP → 

Ln(Z) = a·Ln(P) + C → Ln(Z/P^a) = C → ...

(P^[((n - 1) / n)) - m]) / Z = constante

Nos referiremos de aquí en adelante a este conjunto de relaciones como (6m).

Resumen y conclusión de Schultz en esta sección de análisis diferencial

Las tres relaciones de 6m resultan aproximaciones de la curva "p" del compresor centrífugo, cada una de ellas a través de pares de variables distintas (P-T, P-V, P-Z). Las variables m y n no son estrictamente constantes en un gas real, dependen de Z, Cp, JT, etc. Pero cuando usamos sus valores medios como constantes, todas las trayectorias describen una sola curva politrópica.

Una de estas relaciones es politrópica, ya que describe matemáticamente esta curva, por lo tanto llamamos a e "eficiencia politrópica", a Qp "calor reversible politrópico de entrada al sistema" y a Wp "trabajo neto reversible politrópico de entrada" o "polytropic head".

Otra cuestión importante es que como hemos visto, Schultz no parte de la expresión clásica de proceso politrópico (P·V^n = constante), si no que la define a partir de la expresión de la ecuación 6 (e ≈ V·(dP / dH) = constante). Para él, el proceso politrópico se define por cómo cambia la presión con la entalpía, lo que coincide con su expresión del trabajo y la eficiencia en este proceso. De igual forma, si partimos de la ecuación 6, y desarrollamos todas las relaciones de esta sección, podemos observar como llegamos inevitablemnte a la expresión P·V^n = constante. Es decir, que la expresión clásica de un proceso politrópico (P·V^n = constante) es una consecuencia de la expresión politrópica "energética" de Schultz. La definición politrópica es energética por tanto, y al relación P·V^n = constante es solo su manifestación matemática.

2.3 Test de Evaluación

En este capítulo Schultz traslada el trabajo académico de la sección anterior, análisis diferencial, a la aplicabilidad para el caso real que estamos tratando, el test real de un compresor centrífugo. Con las ecuaciones dieferenciales podemos describir el proceso completo, pero en un test real disponemos de medidas de puntos discretos, entonces, ¿cómo usamos las ecuaciones politrópicas teóricas vistas hasta ahora, con datos reales de un banco de pruebas? Veamos como Schultz nos explica cómo a partir de datos discretos podemos describir la trayectoria interna del proceso.

Para poder despejar la trayectoria "p" de un compresor centrífugo, siendo conocidos dos puntos discretos, tenemos que ser capaces de resolver la ecuación 5, Wp = ∫ V·dP (integral entre los límites P y P0, un punto cualquiera de la curva "p" y punto inicial del compresor o admisión respectivamente). Tenemos que buscar por tanto, las relaciones que nos permitan resolver esta integral para dos puntos, y eso es lo que Schulz nos describe en este capítulo.

Vamos a reorganizar primero las relaciones de 6m:

• A partir de la relación: P^m / T = constante → Si evaluamos dos puntos del mismo proceso (incial y final), la relación debe ser constante para todos los puntos ...

(P^m / T) = (P0 ^m / T0) → donde 0 es el punto inicial de nuestra curva politrópica "p", y el otro punto cualquiera de la curva. Reordenando la expresión ...

(T / T0) = (P / P0)^m = constante → y ahora introduciendo otra relación de 6m

(P^[((n - 1) / n)) - m]) / Z... 

• (P^[((n - 1) / n)) - m]) / Z = constante → Evaluando dos puntos, bajo esta propiedad constante...

(P^[((n - 1) / n)) - m]) / Z = (P0 ^[((n - 1) / n)) - m]) / Z0 = constante → reordenando ...

(Z0 / Z) = (P0 / P)^[((n-1)/n) - m] → {multiplicando a ambos lados por (P0 / P)^m} →

(Z0 / Z)·(P0 / P)^m = (P0 / P)^((n-1)/n) → (P0 / P)^m = (Z / Z0)·(P0 / P)^((n-1)/n) → (P / P0)^m = (Z0 / Z)·(P / P0)^((n-1)/n)

Podemos recombinar finalmente en ...

(T / T0) = (P / P0)^m = (Z0 / Z)·(P / P0)^[(n-1)/n]

• A partir de la relación: P·V^n = constante → Evaluando dos puntos, bajo esta propiedad constante ...

P·V^n = P0·V0 ^n = constante → (V0 / V) = (P / P0)^(1/n) = constante, si ahora introducimos la relación de 6m  (P^[((n - 1) / n)) - m]) / Z ...

• (P^[((n - 1) / n)) - m]) / Z = constante → Evaluando dos puntos, bajo esta propiedad constante...

(P^[((n - 1) / n)) - m]) / Z = (P0 ^[((n - 1) / n)) - m]) / Z0 = constante → reordenando ...

(Z0 / Z) = (P0 / P)^[((n-1)/n) - m] → {trabajando el exponente: (n-1)/n = 1 - (1/n), añadiendo ahora a m ... [(n-1)/n] - m = 1 - (1/n) - m = (1 - m) - (1/n)}, esta forma de reformular el exponente no deja la siguiente expresión ...

(Z0 / Z) = [(P0 / P)^(1 - m)] · [(P0 / P)^(-1/n)] → {sabiendo que: (P0 / P)^(-1/n) = (P / P0)^(1/n) y (P / P0)^-(1 - m) = (P0 / P)^(1 - m)}

tenemos: ... (Z0 / Z)·(P0 / P)^(1 - m) = (P / P0)^(1/n)

Podemos recombinar finalmente en ...

(V0 / V) = (P / P0)^(1/n) = (Z0 / Z)·(P / P0)^(1 - m)

• A partir de las relaciones anteriores: (T / T0) = (P / P0)^m & (V0 / V) = (P / P0)^(1/n) podemos reordenar de la siguiente manera ...
  • (T / T0) = (P / P0)^m → (T / T0)^(1/m) = (P / P0)^[m·(1/m)]
  • (V0 / V) = (P / P0)^(1/n) → (V0 / V)^n = (P / P0)^[n·(1/n)]

(P / P0) = (T / T0)^(1/m) = (V0 / V)^n 

Nos referiremos de aquí en adelante a este conjunto de relaciones como (6n).

Y si seguimos reorganizando las anteriores expresiones de 6n podemos obtener:

• m = log (T / T0) / log (P / P0), expresión después de despejar m de la expresión 1 de las relaciones de 6n.
• n = log (P / P0) / log (V0 / V), expresión después de despejar m de la expresión 1 de las relaciones de 6n.
• m - [(n-1) / n] = log (Z0 / Z) / log (P / P0), expresión después de despejar m de la expresión

(Z0 / Z) = (P0 / P)^[((n-1)/n) - m] usada en las relaciones de 6n.

Nos referiremos de aquí en adelante a este conjunto de relaciones como (6o).

Con estas reordenaciones anteriores y otras relaciones vistas en la sección 2.2, podemos integrar la ecuación 5, de forma aproximada al menos, usando las relaciones vistas en (6f), (6n), (6o) y (13), veámoslo en los siguientes pasos:

*Nota: Puedes saltarte esta explicación sobre los desarrollos de ecuaciones para resolver la ecuación 5, e ir al resumen de la expresión final, llamado 5a.

• Primero, Wp = ∫ V·dP, integral para los límites P y P0  → ∫ V·dP = R · ∫(Z / m)·dT, para los límites T y T0.

Donde esta igualación se explica usando la ecuación 13, P·V = Z·R·T:

• ∫ V·dP = ∫ [(Z·R·T)/P]·dP = {de la expresión 6f-1 sabemos que (P/T)·(dT/dP) = m}

(P/T)·(dT/dP) = m → dP = [P/(T·m)]·dT, sustituyendo entonces ...

∫ [(Z·R·T)/P]·dP = ∫ [(Z·R·T·P)/(T·m·P)]·dT = ∫ [(Z·R)/(m)]·dT →

Wp = ∫ V·dP = R · ∫(Z / m)·dT

• Segundo, Aproximamos la integral de la siguiente forma:

Wp = ∫ V·dP = R · ∫(Z / m)·dT → 

Wp ≈ [n / (n-1)]·P0·V0[(P/P0)^[(n-1) / n] - 1] = 

[n / (n-1)]·Z0·R·T0·[(T/T0)^[(n-1) / (m·n)] - 1]

Esta aproximación a ambos lados del igual es posible teniendo en cuenta los desarrollos de cada una de las integrales de las siguientes formas:

• ∫ V·dP → {de la relación 6n-2 tenemos: V0/V = (P/P0)^(1/n) → V0·(P0/P)^(1/n) = V, podemos sustituir a V de la integral} → ∫ V·dP = 

∫ V0·(P0/P)^(1/n)·dP = V0 · ∫ (P0/P)^(1/n)·dP = V0 · P0^(1/n) · ∫ P^(-1/n)·dP → {donde ∫ P^(-1/n)·dP = [n/(n-1)] · P^[(n-1)/n], pendiente de evaluar este resultado de la integral entre P y P0} → 

V0 · P0^(1/n) · ∫ P^(-1/n)·dP = V0 · P0^(1/n) · [n/(n-1)] · [ P^[(n-1)/n] - P0^[(n-1)/n] ] = V0 · P0^(1/n) · [n/(n-1)] · P0^[(n-1)/n] · [ P^[(n-1)/n] - 1 ] = V0 · P0^[(1/n)-(1/n)] · [n/(n-1)] · [ P^[(n-1)/n] - 1 ] = [n/(n-1)] · V0 · P0 · (P^[(n-1)/n] - 1 )

Por esto finalmente podemos expresar que:

∫ V·dP ≈ [n/(n-1)] · V0 · P0 · (P^[(n-1)/n] - 1 ), y ponemos el símbolo de equivalencia ya que estamos suponiendo que n es constante.

• R · ∫(Z / m)·dT → {de la relación 6n-2 tenemos: (P / P0)^(1/n) = (Z0 / Z)·(P / P0)^(1 - m). Y con la relación 6n-1 tenemos:  (P / P0) = (T / T0)^(1/m)}
  • Reformulación de la ecuación 6n-2: (P / P0)^(1/n) = (Z0 / Z)·(P / P0)^(1 - m) → (Z0 / Z) = (P / P0)^[(1/n) + m - 1] → (Z0 / Z) = (P / P0)^[(m·n +1 - n)/n]
  • Recombinando 6n-2 con 6n-1: (P / P0) = (T / T0)^(1/m) para sustituir (P / P0) en 6n-2 → (Z0 / Z) = (P / P0)^[(m·n +1 - n)/n] = (T / T0)^[((m·n +1 - n)/n) · (1/m)] → Z = Z0 · (T / T0)^[ (-m·n -1 + n)/(n·m)] = Z0 · (T / T0)^[(n-1 - m·n)/(n·m)]  

Con estos desarrollos de 6n-1 y 6n-2 podemos hacer la siguiente sustitución en la relación R · ∫(Z / m)·dT:

• R · ∫(Z / m)·dT = (R/ m) · ∫ Z·dT = (R/ m) · ∫ Z0 · (T / T0)^[(n-1 - m·n)/(n·m)] · dT → (R/ m) · Z0 ·∫(T / T0)^[(n-1 - m·n)/(n·m)] · dT

​​​​​​​Si ahora nos centramos en la integración:

• ∫(T / T0)^[(n-1 - m·n)/(n·m)] · dT, para los límites de la integral T y T0 → podemos plantear el siguiente cambio de variable: 

x = (T / T0), donde si derivamos a ambos lados ... dx = (dT / T0) → T0·dx = dT.

Y respecto a los límites de la integral, con este cambio de variable de x = (T / T0) = x(T) tendríamos lo siguiente: 

• Límite superior: x(T = T) = T / T0
• Límite inferior: x(T = T0) = T / T0 = 1

Además de lo anterior, para mayor simplicidad en el manejo del exponente, podemos darle la siguiente forma: [(n-1 - m·n)/(n·m)] = (n-1)/(n·m) +1. Teniendo en cuenta esta expresión, podemos usar una variable para recoger el exponente, como: a = (n-1)/(n·m), quedando el exponente espresado como a -1 finalmente.

Entonces, podemos reescribir la integral como:

∫(T / T0)^[(n-1 - m·n)/(n·m)] · dT = T0 · ∫ x ^ (a-1) · dx

Y la resolución de esta integral quedaría de la siguiente forma:

∫ x ^ (a-1) · dx = [x^(a-1+1)] / a, evaluado entre T / T0 y 1. Con lo que la forma final de la integral después de evaluarla en sus límites sería:

∫ x ^ (a-1) · dx = [x^(a-1+1)] / a = (1/a) · [(T / T0)^a - 1^a] = (1/a) · [(T / T0)^a - 1] = ((n·m)/(n-1)) · [(T / T0)^(n-1)/(n·m)] - 1]

Volviendo entonces a R · ∫(Z / m)·dT, reordenamos con lo visto anteriormete:

R · ∫(Z / m)·dT = (R·Z0·T0)/m · (n·m)/(n-1) · [(T / T0)^[(n-1)/(n·m)] - 1] →

R · ∫(Z / m)·dT ≈ n/(n-1) · Z0·R·T0 · [(T / T0)^[(n-1)/(n·m)] - 1], y ponemos el símbolo de equivalencia ya que estamos suponiendo que n y m son constante.

Y de esta forma es como se deduce la expresión Wp ~ [n / (n-1)]·P0·V0·[(P/P0)^[(n-1) / n] - 1] = 

[n / (n-1)]·Z0·R·T0·[(T/T0)^[(n-1) / (m·n)] - 1].

Pero Schultz sigue desarrollando esta equivalencia de la siguiente manera:

• [n / (n-1)]·Z0·R·T0·[(T/T0)^[(n-1) / (m·n)] - 1] → {usando la expresión de 6n-3: (P / P0) = (T / T0)^(1/m). Podemos sustituir el cociente (T/T0)} → (T/T0)^[(n-1)/(m·n)] = (T/T0)^(1/m)^[(n-1)/n] = (P / P0)^[(n-1)/n]

Por la sustitución anterior tenemos: 

[n / (n-1)]·Z0·R·T0·[(T/T0)^[(n-1) / (m·n)] - 1] =  [n / (n-1)]·Z0·R·T0·[(P / P0)^[(n-1)/n] - 1]

• [n / (n-1)]·P0·V0[(P/P0)^[(n-1) / n] - 1] → {usando la expresión de 6n-1: (T / T0) = (Z0 / Z)·(P / P0)^[(n-1)/n]. Podemos sustituir la expresión (P/P0)^[(n-1)/n]} → (P / P0)^[(n-1)/n] = (Z·T)/(Z0·T0)

Por la sustitución anterior tenemos: 

[n / (n-1)]·P0·V0[(P/P0)^[(n-1) / n] - 1] =  [n / (n-1)]·P0·V0[(Z·T)/(Z0·T0) - 1]

• [n / (n-1)]·P0·V0[(Z·T)/(Z0·T0) - 1] → {usando la expresión 13: P·V = Z·R·T. Podemos tener la expresión (P·V)/(P0·V0) = (R·Z·T)/(R·Z0·T0) = (Z·T)/(Z0·T0)}

Por la sustitución anterior tenemos:

[n / (n-1)]·P0·V0[(Z·T)/(Z0·T0) - 1] = [n / (n-1)]·((P0·V0)·(P·V)/(P0·V0) - P0·V0) = [n / (n-1)] · (P·V - P0·V0)

• [n / (n-1)] · (P·V - P0·V0) → {usando la expresión 13: P·V = Z·R·T}

Tenemos:

[n / (n-1)] · (P·V - P0·V0) = [n / (n-1)] · (Z·R·T - Z0·R·T0) = [n / (n-1)] · R · (Z·T - Z0·T0)

• [n / (n-1)] · (P·V - P0·V0) → {usando la expresión 6o-2: n = log (P / P0) / log (V0 / V). Podemos tener las expresiones: 1) n - 1 = [ log(P / P0) - log(V0 / V) ] / log(V0 / V), 2) log(V0 / V) / [ log(P / P0) - log(V0 / V) ], 2) n / (n-1) = log(P / P0) / [ log(P / P0) - log(V0 / V) ] = log(P / P0) / log(P·V / P0·V0)}

Por la sustitución anterior tenemos:

[n / (n-1)] · (P·V - P0·V0) = log(P / P0) · [(P·V - P0·V0) / log(P·V / P0·V0)] 

• log(P / P0) · [(P·V - P0·V0) / log(P·V / P0·V0)]  → {usando la expansión de Taylor: ln(A / B) ≈ (A - B) / [(A + B) / 2]. Podemos tener la expresión [(A - B) / ln(A / B)] ≈ (A + B) / 2, esta aproximación es aplicable para A ≈ B, es decir, para cambios pequeños. Lo que para A = P·V y B = P0·V0, aplicaría a decir: P·V ≈ P0·V0, para cambios muy pequeños en la curva "p", que podrían aplicarse con métodos numéricos por ejemplo al iterar con puntos aproximados, buscando emular una inetgración de amplitudes infinitesimales. Aplicar expansión de Taylo requiere pasar de base logarítmica a base neperiana primero, por eso se podrá apreciar un neperiano en la expresión final.}

Por la sustitución anterior tenemos:

log(P / P0) · [(P·V - P0·V0) / log(P·V / P0·V0)] ~ ln(P / P0) · [(P·V + P0·V0) / 2]

• ln(P / P0) · [(P·V + P0·V0) / 2]  → {para n = 1 y recordando que P·V ^n = cte → P·V = P0·V0}

Por la sustitución anterior tenemos:

ln(P / P0) · [(P·V + P0·V0) / 2] = ln(P / P0) · P0·V0  →

Wp ≈ P0·V0 · ln(P / P0), para n = 1

Resumiendo las anteriores relaciones y desarollos vistos tenemos:

•  Wp = ∫ V·dP = R · ∫(Z / m)·dT
• Wp ≈ [n / (n-1)]·P0·V0[(P/P0)^[(n-1) / n] - 1] = [n / (n-1)]·Z0·R·T0·[(T/T0)^[(n-1) / (m·n)] - 1]
• Wp ≈ [n / (n-1)]·Z0·R·T0·[(T/T0)^[(n-1) / (m·n)] - 1] = [n / (n-1)]·P0·V0[(Z·T)/(Z0·T0) - 1]
• Wp ≈ [n / (n-1)] · (P·V - P0·V0) = [n / (n-1)] · R · (Z·T - Z0·T0)
• Wp ≈ log(P / P0) · [(P·V - P0·V0) / log(P·V / P0·V0)] ~ ln(P / P0) · [(P·V + P0·V0) / 2]
• Wp ≈ P0·V0 · ln(P / P0), para n = 1

Nos referiremos de aquí en adelante a este conjunto de relaciones como (5a).

Otro resultado útil de la prueba es el "polytropic head cofficient". Recordemos que Schultz usa el término "head" para denotar la energía o trabajo del compresor, siendo Wp el trabajo politrópico reversible neto al compresor, también llamado "polytropic head" por Schultz. Volviendo a este coeficiente, es útil para relacionar el head del compresor con su velocidad de la siguiente forma:

• μ = (g· Wp) / ∑ u^2  (26)

Donde g es la aceleración de la gravedad (9,81 m/s^2) y u el "impeller rim speed", lo que es la velocidad tangencial en el extremo del impulsor de un compresor centrífugo. Recordemos que la velocidad tangencial se puede expresar como: u = ω · radio.

Este coeficiente que relaciona el trabajo con la velocidad del impeller, permite unir el diseño termodinámico del compresor con su diseño mecánico como, rpm del compresor, diámetro de los impellers, etc... gracias a la evaluación de la velocidad, todo esto lo veremos en secciones posteriores con mayor detalle.

El sumatorio es tomado sobre el número de impulsores dentro del compresor centrífugo. Para el hipotético test que sigue la descripción de Schultz tenemos 3 etapas:

• μ = (g· Wp) / [ u1^2 + u2^2 + u3^2 ]  (26a)

Donde si todos los impulsores del compresor tuvieran el mismo diámetro (y por tanto la misma velocidad tangencial):

• μ = (g· Wp) / [ 3·u^2 ]  (26b)

μ por tanto, evalúa cómo de eficaz es el compresor para convertir velocidad (energía cinética del rodete) en trabajo de compresión. Tenemos que tener en cuenta que cada etapa puede tener su propio coeficiente (μ1, μ2 y μ3 para nuestro caso), donde cada uno puede ser calculado a partir del cálculo del trabajo de cada etapa, y de la velocidad de cada etapa. Si todas las etapas del compresor son geométricamente iguales, y todas trabajan con la misma eficiencia, entonces todas tienen el mismo coeficiente en cada etapa. Siendo esto último una propiedad de las ecuaciones (5), (6) y (26).

Para finalizar esta sección Schultz enfatiza, que pese todos los desarrollos anteriores sobre el análisis politrópico, el procedimiento de test de un compresor centrífugo es simple y se puede resumir como:

1. Determinar P, V y H en la entrada y la salida del compresor, lo que en el ejemplo de Schultz serían los puntos 0 y 3. Schultz no explica como determinar estas tres variables, pero en un test real tanto la presión como la temperatura pueden ser medidas directas, mientras que el volumen expecífico y la entalpía son funciones de estado, que pueden ser evaluadas con tablas o cualquier software de termodinámica como este. El cálculo de estas variables de forma analítica será visto en detalle en la sección 2.6.
2. Una vez lo anterior calcular:

• n = log (P3 / P0) / log (V0 / V3)
• Wp ≈ [n / (n-1)] · (P3·V3 - P0·V0)
• e = Wp / (H3 - H0)
• μ = (g· Wp) / [ u1^2 + u2^2 + u3^2 ]

Nos referiremos de aquí en adelante a este conjunto de relaciones como (27)

La precisión de Wp in las relaciones de 27 dependede de los constante que sea n a lo largo de la curva p. A lo largo de este artículo explicaremos como Schultz dispone de otros medios para minimizar esta dependencia de esta idealización de constancia para n.

De esta forma es como Schultz obtiene el trabajo politrópico de un compreso centrífugo a partir de medidas directas.

2.4 Análisis isentrópico

En esta sección Schultz nos demuestra por qué el análisis isentrópico resulta limitado para describir la curva real de compresión frente a un análisis politrópico, y esto más agravado en compresores multietapa. Antes de comenzar con el desarrollo de esta sección vamos a explicar el contexto de la curva isentrópica que Schultz refleja en el diagrama (curva S0 de la figura 1), ya que esta curva solo está delimitada por 0 y 4, a diferencia de las tres etapas de la curva politrópica "p" (0, 1, 2 y 3). Esto se debe a que en el proceso politrópico tenemos pérdidas en cada una de las etapas, mientras que la curva isentrópica es una curva ideal equivalente, es decir, que es una curva que describe un proceso adiabático y reversible que parte de 0 y llega a la misma presión final, 4.

Hasta el momento nos hemos centrado en el análsis politrópico, pero exísten otros análisis termodinámicos para un compresor centrífugo llamados "adiabático" o "isentrópico". Estos difieren del análisis politrópico para poder sustituir el trabajo isentrópico o "isentropic head", Ws, por  el trabajo politrópico o "polytropic head", Wp. El trabajo isentrópico de un compresor es la energía de entrada neta requerida por una compresión adiabática y reversible, que tiene el mismo estado inicial (T y P) y presión final que una compresión politrópica. La ruta o curva de un proceso de compresión adiabática reversible es isentrópica.

Para el hipotético test del compresor de tres etapas ejemplificado por Schultz, mostrado en la figura 1, esta ruta es S0 y su trabajo isentrópico se puede desarrollar con las siguientes relaciones:

• Ws = H4 - H0, este sería el trabajo mínimo teórico paa alcanzar la presión en 4, que es la misma presión que en 3 de la curva p. Mínimo trabajo teórico, ya que no se tiene en cuenta rendimientos.
• P4 = P3
• S4 = S0, lógico al ser una curva isentrópica.

*Nota: no confundir "4" con una nueva etapa, Schultz usa este nuevo número para etiquetar las condiciones de descarga isentrópicas de la compresión, y no confundir con 3 (descarga politrópica).

Nos referiremos de aquí en adelante a este conjunto de relaciones como (28)

A través de las relaciones de 5a y 6o, las ecuaciones de 28 pueden ser aproximadas a una forma politrópica como:

• ns = log (P4 / P0) / log (V0 / V4)
• Ws ≈ [ns / (ns - 1)] · (P4·V4 - P0·V0)

Nos referiremos de aquí en adelante a este conjunto de relaciones como (28a)

La precisión de Ws en las relaciones de 28a depende de cómo de constante sea ns a lo largo de la cruva S0.

La eficiencia isentrópica se describe como:

• es = (H4 - H0) / (H3 - H0) = Ws / (W - ΔKE)  (29)

Y el coeficinte de trabajo isentrópico o "isentropic head coefficient" es:

• μs = (g· Ws) / ∑ u^2 = g· (H4 - H0) / [ u1^2 + u2^2 + u3^2 ]   (30)

Las eficiencias de las etapas isentrópicas y los coeficientes de trabajo, pueden evaluarse a partir de los trabajos y velocidades de cada etapa individual.
Sin embargo, a diferencia de sus homólogos politrópicos, las eficiencias de las etapas isentrópicas iguales y los coeficientes de trabajo de etapas isentrópicas iguales, deben superar es y μs para el compresor en su conjunto. Esta disparidad aumenta a medida que aumenta la relación de compresión o el número de etapas y se varía de un gas a otro. Esto provoca que mientras en el análisis politrópico deciamos que μ = μ1 = μ2 = μ3 cuando las etapas eran geométricamente iguales y trabajan con la misma eficiencia, en el análisis isentrópico esto no se cumple.

Esta dificultad puede atribuirse a la relación general de la termodinámica (segundo principio de la termodinámica exactamente) requieriendo que las líneas de presión diverjan sobre un gráfico de Mollier (este es el típico diagrama de entalpía VS entropía, muy usado en turbomáquinas).

• (∂H/∂S)P = T  (31), donde proviene de la expresión: dH = V·dP + T·dS, para P cte.

Con la ecuación 31 estamos diciendo que a presión constante la pendiente dH/dS es la temperatura, y como T cambia con la presión, las líneas de presión que se dibujan sobre una gráfica H-S (gráfico de Mollier) pues no son paralelas. A cambios iguales de entropía, no se producen los mismos cambios de entalpía a distintas presiones. Este es el comportamiento que hace que las pérdidas isentrópicas no se sumen linealmente en multietapas, ya que cada etapa tiene su nivel de presión diferente, y su misma delta de entropía no produce el mismo delta de entalpía en todas las etapas.

Como consecuencia, Schultz recomienda el análisis politrópico para test, diseño y extrapolación a otros gases o compresores. El análisis isentrópico es correcto, pero como una referencia teórica.

2.5 Factor de Trabajo Politrópico o "Polytropic Head Factor"

A pesar de las deficiencias del análisis isentrópico vistas anteriormente, este tiene una ventaja: Ws en la ecuación de (28) se muestra exacta, a diferencia de Wp en (5a) y (27) donde se muestra aproximada. Además de esto, en (28a) Ws se fuerza a una forma similar a la curva politrópica dando lugar a una equivalencia. Es decir, que para Ws tenemos una ecuación exacta y otra aproximada, y esto nos permite conocer de forma precisa la diferencia o error entre su valor exacto y su aproximado. Recordemos que la forma aproximada de Ws en (28a) era:

• Ws ≈ [ns / (ns - 1)] · (P4·V4 - P0·V0)

Y la forma exacta en (28) era:

• Ws = H4 - H0

Con lo que en la ecuación (28a) hay un error relativo respecto a la ecuación (28), debido a que ns no es contante a lo largo de la curva S0 en la aproximación hecha en Ws.

Schultz nota que pasa algo parecido para Wp, tenemos su forma exacta en la ecuación (5):

• Wp = ∫ V·dP

Y tenemos su forma aproximada en la ecuación (5a):

• Wp ≈ [n / (n-1)] · (P·V - P0·V0)

Con la diferencia ahora, que para la forma exacta no podemos resolver la expresión. Pero para la forma aproximada de Wp tenemos las mismas aproximaciones que para Ws: n constante y Z tratada de forma promedio. Los errores relativos de ambas curvas tienen el mismo orígen matemático, ya que ambas expresiones dependen de la curvatura real del gas y ambas usan exponentes promedios (n y ns).

Si aplicamos el error relativo de Ws a Wp, nos acercaremos mucho al valor exacto de Wp. Realizar esta afirmación no se trata de una mera aproximación, sino de una propagación del error controlada.

Y el error relativo a la expresión real lo podemos calcular entonces a partir de Ws, dividiendo su forma exacta entre su forma aproximada. Acorde a esto se define el factor de trabajo politrópico:

• f =  (H4 - H0) / [(ns / (ns - 1)) · (P4·V4 - P0·V0)]   (32)

El cual es la división de la ecuación de (28) entre la ecuación (28a).

Multiplicando la forma aproximada de Wp de las ecuaciones de (5a) o de la (27) por este coeficiente f, podemos aproximarnos a la forma exacta de Wp espresada en la ecuación (5), independientemente de la constancia de n a lo largo de la curva p. Una aproximación más estrecha podría ser obtenida si f fuera determinada a lo largo de S1 o S2, pero S0 es más conveniente y debería ser suficiente. En muchas ocasiones este coeficiente f está tan cercano a la unidad que su impacto en el trabajo final resulta muy pequeño.

Si ahora introducimos este factor en el resumen de ecuaciones del test de evaluación, es decir, las ecuaciones de 5a, podemos pasar las relaciones equivalentes de Wp a relaciones extactas:

• Wp = f · [n / (n-1)]·P0·V0[(P/P0)^[(n-1) / n] - 1] = f · [n / (n-1)]·Z0·R·T0·[(T/T0)^[(n-1) / (m·n)] - 1]
• Wp = f · [n / (n-1)]·Z0·R·T0·[(P/P0)^[(n-1) / (n)] - 1] = f · [n / (n-1)]·P0·V0[(Z·T)/(Z0·T0) - 1]
• Wp = f · [n / (n-1)] · (P·V - P0·V0) = f · [n / (n-1)] · R · (Z·T - Z0·T0)
• Wp = f · log(P / P0) · [(P·V - P0·V0) / log(P·V / P0·V0)] ~ f · ln(P / P0) · [(P·V + P0·V0) / 2], donde se sigue manteniendo la última equivalencia ya que se había aplicado la expansión de Taylor, puedes volver a repasar esto en las relaciones de (5a).
• Wp = f · P0 · V0 · ln(P / P0), para n = 1

= (HS - H0) / [(ns / (ns - 1)) · (P·VS - P0·V0)]

• ns = log(P/P0) / log(V0/VS)

Nos referiremos de aquí en adelante a este conjunto de relaciones como (5b).

El procedimiento de test de un compresor centrífugo puede resumirse ahora como:

1. Determinar P, V y H en la entrada y la salida del compresor, es decir, en los puntos 0 y 3. Donde el volumen específico y la entalpía pueden ser calculadas como funciones de estado a partir de las tomas de presión y temperatura en ambos puntos. La determinación de estas variables de forma analítica se verá con detalle en la sección 2.6.
2. Una vez lo anterior calcular:

• n = log (P3 / P0) / log (V0 / V3)
• ns = log (P3 / P0) / log (V0 / V4), como las presiones en 3 y 4 son iguales podemos dejar la presión en 3, en cambio al no ser la temperatura la misma en 3 que en 4, para el volumen específico ya hay que poder el de 4.

= (H4 - H0) / [(ns / (ns - 1)) · (P3·V4 - P0·V0)]

• Wp = f · [n / (n-1)] · (P3·V3 - P0·V0)
• e = Wp / (H3 - H0)
• μ = (g· Wp) / [ u1^2 + u2^2 + u3^2 ]

Nos referiremos de aquí en adelante a este conjunto de relaciones como (27a).

En las ecuaciones de (5b) y (27a) Wp es prácticamente independiente de la mayor o menor constancia de n a lo largo de la curva p. También es importante destacar, que las ecuaciones  de (27a) se limitan a pruebas de compresores centrífugos sin refrigeración y sin flujo lateral. En un compresor centrífugo ideal entra un caudal ṁ0, igual al que sale, ni sale ni entra masa entre etapas. En un compresor centrífugo real en cambio, se inyecta o extrae gas entre etapas por purgas, reciclados, inyección de gas frío, bypass, etc... Con lo que en un compresor centrífugo real la masa no es contante a lo largo de la curva p, y la temperatura tampoco al poder llevar etapas de enfriamiento entre las etapas del compresor.

Schultz trata estas mismas expresiones vistas hasta ahora, teniendo en cuenta etapas de enfriamiento y de flujo lateral en secciones posteriores de este mismo artículo, lo veremos más adelante.

2.6 Diseño de Compresores

En esta sección Schultz aborda como poder diseñar un compresor centrífugo real cuando no se dispone de tablas termodinámicas completas del gas en cuestión, y por otra parte, como hacerlo cuando sí se dispone de tablas y gráficas de propiedades termodinámicas. Esto nos será útil para comprender nuestros métodos de cálculo en la actualidad mediante software.

No olvidemos que esta publicación es de 1962, cuando los cálculos eran manuales y no había posibilidad de realizar iteraciones y métodos numéricos mediante ordenador para despejar variables. Esta es la razón de ser de esta sección, orientar al diseñador mediante una serie de ecuaciones y pasos, algo que a día de hoy haremos en un software de termodinámica, pero que sigue siendo un tesoro para entender el proceso de resolución de estos problemas.

Entonces volviendo al problema objetivo planteado por Schultz, solo se conocen condiciones iniciales y finales de presión, y algunas otras propiedades medias. Es decir, partimos del conocimiento de estas variables:

• Condiciones de entrada: P0 y T0.
• Condiciones de salida: P3.

Y el diseñador quiere calcular:

• Trabajo politrópico, Wp.
• Trabajo real, W.
• Velocidad periférica, μ.
• Número de etapas necesarias para alcanzar P3.
• Estados de salida: V3 y T3.

Todo lo anterior sin conocer la curva termodinámica exacta del gas. Schultz nos expone entonces varias formas de calcular las variables de diseño del compresor, en fucnión del nivel de información del que dispongamos. Las soluciones que nos explica en esta sección, pasan por usar el análisis politrópico como herramienta de diseño. Comencemos entonces.

Caso en el que no se dispone de tablas y gráficas termodinámicas del gas real en cuestión

Ecuaciones similares a las relaciones de (27a) pueden ser empleadas para diseñar compresores centrífugos cuando no están disponibles tablas termodinámics detalladas o gráficas del gas objeto del diseño. El problema es determinar las variabes W, u, el número de etapas, V0, V3, y T3 a partir de las variables iniciales conocidas de P0, T0, y P3. Recopilando las relaciones de (4), (5b), (6h), (13) y (26) podemos obtener:

• m = (Z·R / Cp) · [(1/e) + X] = [((k - 1) / k) · ((1/e) + X) · Y] / (1 + X)^2, vista explícitamente en (6h).
• n = 1 / (Y - m · (1 + X)) = (1 + X) / [Y · [(1 / k) · ((1/e) + X) - ((1/e) - 1)]], vista explícitamente en (6h).
• Wp = f · [n / (n-1)]·Z0·R·T0·[(P/P0)^[(n-1) / (n)] - 1], vista explícitamente en (5b).
• W = (Wp / e) + ΔKE, vista implícitamente en (4).
• ∑ u^2 = (g· Wp) / μ, vista implícitamente en (26).
• V0 = Z0·R·T0 / P0, vista implícitamente en (13).
• V3 = V0 / (P3/P0)^1/n, vista implícitamente en (6m).
• T3 = T0 · (P3/P0)^m, vista implícitamente en (6m).

Nos referiremos de aquí en adelante a este conjunto de relaciones como (33).

Estas relaciones de (33) son creadas por Schultz para poder pasar de las variables iniciales comentadas, a las variables objetivo. Usando para ello: n, m, suposiciones razonables para e y μ, y siendo conocidas las propiedades medias del gas (Cp, X, Y y Z).

Parece un poco confuso pensar que en este ejemplo de Schultz el diseñador no tiene tablas de propiedades, pero en cambio si tiene unos valores medios del gas como Cp, X, Y y Z. Bueno, esto es plausible pensando que hay valores ingenieriles típicos tabulados por familias de gases, lo cuales eran muy usados cuando no había software. Por ejemplo, es posible que estés habituado a ver en libros de texto de termodinámica básica, que Cp para gases ideales es igual a 1,40.

Schultz matiza esto explicando que para las relaciones de (33) se estima un valor medio de Cp o k a partir de los datos termodinámicos disponibles. Los valores medios de X, Y y Z se obtienen a partir de gráficos de compresibilidad generalizados para gases en los estados correspondientes, al igual que Z0 en la entrada del compresor. Es decir, que no son las propiedades del gas real en sus condiciones reales, solo valores ingenieriles aproximados. Para obtener la mayor precisión posible, se requiere una solución de prueba y error (un cálculo iterativo), es decir, se debe suponer la temperatura de descarga T3 para estimar los valores medios de X, Y y Z mediante estas tablas generalizadas, y luego ir despejando las ecuaciones de las relaciones de (33) una a una, hasta llegar a la última donde despejamos T3 y podemos comprobar si se aproxima a nuestro valor iterado. Con lo que el método iterativo a seguir deberá ser:

1. Suponer una T3.
2. Cálculo de valores medios a partir de tablas generalizadas.
3. Recálculo de T3 a través de las relaciones de (33).
4. Repetir el proceso hasta converger, es decir, que la T3 supuesta sea la misma que la recalculada.

Notas importantes a la hora de usar valores generalizados: La selección de e y μ se basa en datos de pruebas y en la experiencia. La suposición habitual para f es la unidad. Con frecuencia, ΔKE es insignificante. La separación de u del número de etapas en ∑ u^2 implica consideraciones que no son pertinentes para este análisis preliminar, donde nuestro objetivo no es decidir el diámetro del impulsor, las rpm, ni cómo se reparte el trabajo por etapas, ya que esto entraría dentro del diseño mecánico de compresor, y no en una evaluación termodinámica como estamos llevando a cabo.

Por todo lo anterior, hay que decir que la solución del problema mediante las relaciones de (33) no buscaba una exactitud termodinámica, pero sí un diseño preliminar para que el diseñador pueda saber si las condiciones de diseño eran plausibles termodinámicamente.

Caso similar al anterior, pero disponemos de menos propiedades termodinámicas aún

Una forma alternativa a las relaciones de (33) supone eliminar Y pero requiere añadir Z3 (en las relaciones (33) usábamos Z promedio):

• m = (Z·R / Cp) · [(1/e) + X]
• Wp ≈ [(Cp · T0) / ((1/e) + X)] · [(P/P0)^m  - 1]
• W = (Wp / e) + ΔKE
• ∑ u^2 = (g· Wp) / μ
• V0 = Z0·R·T0 / P0
• T3 = T0 / (P3/P0)^m
• V3 = Z3·V0 / Z0·(P3/P0)^(1-m)

Nos referiremos de aquí en adelante a este conjunto de relaciones como (33a).

Schultz propone esta relación (33a) como un método alternativo y más simple al del uso de las relaciones de (33), ya que introduce Z3 y elimina Y, además de usar una forma aproximada para Wp. Una alternativa que puede ser útil cuando el diseñador tiene aún menos datos disponibles.

Caso en el usamos Cp, X y e constantes y sin iterar T3

Todas las relaciones diferenciales para el análisis politrópico, abren varias soluciones alternativas que surgen de pequeñas congeturas para aproximar la solución. Una de estas es la que hace Schultz, al preguntarse qué pasa si suponemos Cp, X y e constantes, sin falta de tener que acualizar su valor en cada iteración de T3. La respuesta es que el trabajo politrópico queda en una ecuación muy sencilla y casi proporcional al salto térmico. Los resultados provienen de una versión de las relaciones de (5a) en la cual integramos (5) aproximándola por (6f), (6h), (6n) y (13) asumiendo Cp, X y m relativamente constantes comparados a P y T. Observemos el desarrollo de Schultz:

• Wp = R · ∫ (Z / m) · dT, integral evaluada entre los límites de T y T0.

Esta expresión proviene de la ecuación 5 {Wp = ∫ V·dP}, la cual puede ser sustituida por la ecuación 13 {P·V = Z·R·T} de la siguiente forma → ∫ V·dP = ∫ [(Z·R·T)/P]·dP

Una vez planteado lo anterior podemos usar la expresión 6f-1 {(P/T)·(dT/dP) = m} de la siguiente forma:

• (P/T)·(dT/dP) = m → dP = [P/(T·m)]·dT 

Sustituyendo entonces en la ecuación 5 {Wp = ∫ V·dP} todo lo anterior ...

∫ [(Z·R·T)/P]·dP = ∫ [(Z·R·T·P)/(T·m·P)]·dT = ∫ [(Z·R)/(m)]·dT →

Wp = ∫ V·dP = R · ∫(Z / m)·dT

• Wp = ∫ Cp / ((1/e) + X) · dT, integral evaluada entre los límites de T y T0.

Esta expresión se explica usando la ecuación 6h-1 {m = (Z·R / Cp) · [(1/e) + X]} y sustituyendo de forma directa m en la ecuación Wp = R · ∫(Z / m)·dT.

• Wp ≈ Cp · (T - T0) / [(1/e) + X]

Esta expresión se explica asumiendo que las variables Cp, e y X son constantes con el cambio de temperatura, lo cual es toda una aproximación, pero que nos vale para resolver la integral de la siguiente forma:

[Cp / ((1/e) + X)] · ∫ 1 · dT = T entre los límites de T y T0 → [Cp / ((1/e) + X)] · (T - T0)

• Wp ≈ [ (Cp · T0) / ((1/e) + X) ] · [(P/P0)^m - 1]

Esta expresión se puede explicar factorizando el término (T - T0) de la siguiente forma → (T - T0) = T0 · [(T / T0)+ 1]. De esta forma podemos usar la ecuación 6n-1 {(T / T0) = (P / P0)^m} para realizar una sustitución de forma directa: 

Wp ≈ Cp · (T - T0) / [(1/e) + X] = [ (Cp · T0) / ((1/e) + X) ] · [(T / T0)+ 1] = [ (Cp · T0) / ((1/e) + X) ] · [(P/P0)^m - 1] 

Nos referiremos de aquí en adelante a este conjunto de relaciones como (5c).

Con la relación (5c-2), podemos conocer el trabajo politrópico en función de la presión, muy útil en un diseño preliminar.

De forma similar a (5c), podemos tener una nueva versión para la ecuación (6) conteniendo las relaciones de (6f), (6h) y (13):

• dH / dT = Cp / (1 + e·X)   (6p)

Para cualquier gas homogeneo la relación (6p) debe mantenerse a lo largo de una trayectoria de eficiencia constante. Una integración aproximada de (6p) es:

•  H - H0 ≈ Cp · (T - T0) / (1 + e·X)   (6q)

Donde Cp y X se han asumido contantes a lo largo de la curva p.

Caso para el cálculo de valores de diseño etapa por etapa

Hasta aquí hemos visto diferentes modelos de ecuaciones para hallar los parámetros de diseño de un compresor centrífugo real, ahora Schultz nos concreta las relaciones para hacer un diseño etapa por etapa. Habiendo entonces determinado u por las relaciones (33) y (33a), un análisis etapa por etapa es requerido para determinar los valores de salida de cada etapa en cuanto a P, V y T, desde los valores de entrada de cada una de las etapas con los valores conocidos P0, V0 y T0. para este propósito (33) y (33a) son modificados por:

• Wp = μ · (u^2) / g
• P ≈ P0 · ( [((n-1) / n)·Wp / P0V0] + 1 )^(n / (n-1)) ~ P0 · ( [(1/e) + X)·Wp / Cp·T0] + 1 )^(1 / m)

Nos referiremos de aquí en adelante a este conjunto de relaciones como (33b).

Los valores individuales de cada etapa de Cp o k, X, Y, Z, e y μ se emplean para las relaciones de (33b). Es decir, que tenemos que resolver (33b) para cada etapa.

Caso para el cálculo, cuando disponemos de parámetros termodinámicos (tablas, gráficas, software, etc ...), un cálculo un poco más preciso

Cuando tenemos disponibles gráficas detalladas o tablas termodinámicas (hoy en día también disponemos de software de propiedades termodinámicas), el diseñador puede obtener V0 y S0 de forma directa, y de esta forma determinar V3, T3 y H3 desde S3. Recordemos que antes con las relaciones de (33), V0 era obtenido a partir de un proceso iterativo de varias ecuaciones a través de la congetura inical T3. De esta forma ya no necesitamos suponer Z como un valor medio, si no que podemos trabajar directamente con entalpía y entropía. El conocimiento de las distintas formas equivalentes de escribir el diferencial de la entropía en las formas (6), (7) y (13), produce la siguiente expresión para cualquier cualquier gas homogeneo a lo largo de la curva de eficiencia constante: 

• dS / dP = [Z·R / P] · ((1/e) -1)   (6r)

Una aproximación a la integración de la ecuación (6r), usando (6m), es:

• S - S0 ≈ R · ((1/e) -1) · (logP/P0) · [(Z0 - Z) / log(Z0 / Z)] ≈ R · ((1/e) -1) · (lnP/P0) · ((Z0 + Z) / 2)   (6s)

Por ensayo y error la correcta combinación de S3 y Z3 es encontrada en la ecuación (6s). Entonces V3, T3 y H3 pueden ser leídas directamente desde las tablas o gráficas, y W y u calcudas entonces por las relaciones de (2a), (4) y (26). En resumen:

• S - S0 ≈ R · ((1/e) -1) · (lnP/P0) · ((Z0 + Z) / 2)
• W = H - H0 + ΔKE
• Wp = e · (H - H0)
• ∑ u^2 = (g· Wp) / μ

Nos referiremos de aquí en adelante a este conjunto de relaciones como (33c).

El acceso a las propiedades termodinámicas de la entropía y entalpía, nos permite el uso directo de las relaciones de (33c), a partir de la solución aproximada de la integral en (6r), y todo esto desde el marco plitrópico también.

De forma similar para (6r) y (6s) tenemos la siguiente aproximación de solución diferencial de entropía respecto a la temperatura:

• dS / dT = (Cp / T) · [ (1 - e) / (1 + e·X) ]
• S - S0 ≈ Cp · [ (1 - e) / (1 + e·X) ] · (lnT/T0)

Nos referiremos de aquí en adelante a este conjunto de relaciones como (6t).

Estas relaciones de (6t) están desarrolladas a partir de las relaciones de (6f), (6h) y (6r). La ecuación diferencial de (6t) debe mantenerse para cualquier gas homogeneo a lo largo de una curva con eficiencia constante. La resolución aproximada de la integral de (6t) tiene en cuenta como valores medios Cp y X.

Tomando el ratio de (6t) entre (6q) podemos encontrar:

•  e ≈ 1 - [(S3 - S0) / (H3 - H0)] · [(T3 - T0) / ln(T3/T0)]   (27b)

Donde (27b) es otra ecuación del test de evaluación de un compresor centrífugo como (27) y (27a). Aunque (27b) fue descrito desde la ecuación de los gases reales, su precisión es dudosa porque también es una relación de gas ideal. Probablemente sea mejor:

• e ≈ 1 - [(S3 - S0) / (H3 - H0)] · [(Z3·T3 - Z0·T0) / (Z3 - Z0)] · [log(Z0/Z3) / log(Z3·T3 / Z0·T0)]   (27c)

Siendo la ecuación (27c) desarrollada desde las relaciones de (4), (5a), (6s) y (13).

Caso para el cálculo apoyado en la disponibilidad de propiedades termodinámicas, y el uso de relaciones isentrópicas

Otra técnica de diseño con tablas termodinámicas o gráficas es determinar V3 y T3 desde H3, lo cual es encontrado por convertir el análisis politrópico a un análisis isentrópico. Es decir, usaremos la facilidad de cálcular variables de la curva S0, para usarlas en depejar otras de la curva p, como H3, y con ello despejar T3. ¿Por qué hacer esto? la curva isentrópica tiene S0 = S4. y como hemos visto en otros puntos de la publicación P4 = P3. Con P4 y S4 podemos hallar H4, y de esta forma Ws que la usaremos para finalmente calcular H3 ... todo esto nos lo desarrolla Schultz a continuación

La conversión es posible por combinar las relaciones (4), (5b), (6h), (6i), (11), (13), (15c), (16), (18), (22), (26), (29), y (30) para obtener:

• es / e = μs / μ = Ws / Wp = [ns / (ns - 1)] · [(P/P0)^[(ns-1) / (ns)] - 1] / [n / (n - 1)] · [(P/P0)^[(n-1) / (n)] - 1]
• ms = (P·V / Cp·T) · (1 + X) = [(k - 1) / k] · Y / (1 + X) 
• ns = 1 / [Y - ms·(1 + X)] = k / Y
• m = (P·V / Cp·T) · [(1/e) + X] = [(k - 1)/k] · [(1/e) + X] · Y / (1 + X)^2
• n = 1 / [Y - m·(1 + X)] = (1 + X) / (Y · [ (1 / k)·[(1/e) + X] - [(1/e) - 1] ])
• Cp = (ΔH / ΔT)P
• X = [ (T / V) · (ΔV / ΔT)P ] - 1
• Y = (- P / V) · (ΔV / ΔP)T
• Cv = (ΔE / ΔT)V = ( (ΔH - V·ΔP) / ΔT )V = Cp - ( [P·V·(1 + X)^2] / T·Y )
• k = Cp / Cv

Nos referiremos de aquí en adelante a este conjunto de relaciones como (34).

Para las relaciones de (34) los valores necesarios de P, V, T y H para calcular los valores medios de Cp, Cv, k, X e Y son obtenidos desde tablas termodinámicas o gráficas de el gas objeto de diseño. Al igual que antes, e y μ se basan en datos de pruebas y en la experiencia. Hay que tener en cuenta que Cp, Cv, k, X e Y calculados para ms y ns deberían de diferir de los calculados a partir de m y n.

A menudo los valores medios de Cp, X y Z requeridos para calcular ms no difieren de una forma que se aprecie de aquellos requeridos por m. En ese caso, las relaciones de (34) pueden ser simplificadas por (5c) para llegar a ser:

• es / e = μs / μ = Ws / Wp = m · [((P/P0)^ms) - 1] / ms · [((P/P0)^m) - 1]
• ms = (Z·R / Cp) · (1 + X) 
• m = ms · [(1/e) + X] · (1 + X)
• Cp = (ΔH / ΔT)P
• X = [ (T / V) · (ΔV / ΔT)P ] - 1

Nos referiremos de aquí en adelante a este conjunto de relaciones como (34a).

Ambas relaciones, (34) y (34a), reducidas a las ecuaciones de gas ideal considerando X = 0, Y = Z = 1 se pueden expresar como:

• es' = [((P/P0)^ms') - 1] / [((P/P0)^m') - 1], marcamos con apostrofe todas las expresiones aplicadas a gas ideal.
• ms' = (R / Cp) · [(k - 1) / k]
• m' = ms'/e

Nos referiremos de aquí en adelante a este conjunto de relaciones como (34b).

En muchas casos las complicaciones de las relaciones de (34) o incluso de (34a) pueden ser eviatadas por usar (34b) como una primera aproximación para estimar V3' por (35). Con V3 en (27a) se obtiene una e' correspondiente a es'. Entonces tenemos la siguiente relación:

• es' / e' ~ es / e = μs / μ   (34c)

Normalmente la relación es' / e' de (34c) is suficientemente precisa a efectos prácticos. Teniendo hallado es y μs por (34), (34a), o (34c) el diseñador combina las relaciones (28), (29) y (30) para su análisis isentrópico:

• Ws = H4 - H0
• P = Ps
• S4 = S0
• W = (Ws / es) + ΔKE
• ∑ u^2 = (g· Ws) / μs
• H3 = H0 + (Ws / es)

Nos referiremos de aquí en adelante a este conjunto de relaciones como (35).

*Notas importantes: Los valores de P, V, T, H y S para (35) son obtenidos de tablas termodinámicas y gráficos. Y finalmente siendo conocida H3 y P3, vamos a tablas o gráficas (o software en la actualidad) y hallamos T3. Cuando un compresor similar ha sido testeado con el gas objeto de diseño es y μs puede ser deducido directamente desde los datos del test y no sería necesaria una conversión de e y μ.

Es importante mencionar que las ecuaciones (33), (33a), (33b), (33c), (34), (34a), (34b) y (35) son limitadas a el diseño de compresores centrífugos sin refrigeración ni flujo lateral.

Caso para cuando queremos probar un compresor real en taller, pero con otro gas de "prueba" para validar el funcionamiento con el gas objetivo

Una importante aplicación del análisis politrópico es la evaluación del test de eficiencia equivalente, donde un compresor centrífugo diseñado para un gas en particular se prueba en un taller con otro gas diferente. Para duplicar ciertos parámetros de diseño las condiciones del test llegan a ser equivalentes a las condiciones de diseño, y los valores del test de e y μ desde las relaciones (27a) pueden ser usadas en las relaciones (33), (33a) o (33c) para predecir los rendimientos reales obtenidos de un test. Normalmente el análisis isentrópico es impreciso para estos propósitos debido a las dificultades derivadas de la ecuación (31).

Pasando del diseño termodinámico al diseño mecánico real del compresor (velocidad, rpm, diámetro ...)

Uno de los parámetros de diseño de los compresores centrífugos es la velocidad acústica del gas. ¿Por qué nos debería importar este parámetro en un compresor centrífugo para su diseño mecánico? pues resulta que el límite físico del compresor no es térmico para el caso centrífugo, es aerodinámico.

Para una perturbación infinitesimal esto puede mostrarse como:

• a = V · √[-g · (∂P/∂V)s]   (36)

Donde a es la velocidad acústica. Al insertar (13) y (23a) dentro de la ecuación (36) encontramos:

• a = V · √[ns · g · P · V] = √[ (k · g · Z · R · T) / Y ]   (36a)

El diseñador relaciona la velocidad acústica con la velocidad del compresor por un coeficiente de velocidad o "impeller Mach number", M, definido como:

• M = u / a   (37)

Este parámetro M es muy importante, todo compresor centrífugo real se hace imponiendo un Mach máximo admisible (típicamente M ≲ 0,9 en la entrada del impeller). Por eso a es un parámetro clave también, determinando cuándo aparcen choques, cuándo la eficiencia se degrada brutalmente ... definiendonos una velocidad periférica u máxima por esta relación anterior (diseño mecánico).

En la entrada del compresor M se describe como:

• M0 = u1 / a0   (37a)

Ahora si insertamos (5b), (6u), (26) y (36a) dentro de (37a) obtenemos la siguiente expresión:

• 1 + u1·us·(u - 1)·M0^2 / u = (P1/P0)^[(n-1) / n] = (V0/V1)^(n-1) = (T1/T0)^[(n-1) / m·n]    (38)

Donde la primera etapa, donde us es evaluado en la entrada y m y n son valores medios. Para otras etapas aplicarían las mismas relaciones y también para el compresor en su totalidad. Esta ecuación nos dice cuánto salto de presión puede entregar una etapa sin violar el Mach admisible.

A veces es necesario subdividir las etapas individualmente y considerar la eficiencia de las palas (o "impeller") y difusores de forma separada. Schultz separa esto ya que el impeller añade energía al gas, pero el difusor no, solamente recupera presión a cambio de energía cinética, y por esto las pérdidas no están distribuidas igual en ambos componentes mecánicos. Schultz quiere que podamos asignar una eficiencia propia al impeller y otra al difusor, y que ambas queden ligadas y coherentes a la eficiencia global e del compresor que ya hemos tratado durante toda la publicación.

Refiriendonos de nuevo a la gráfica de la figura 1, las curvas politrópicas e isentrópicas, imaginemos que tenemos un punto del test realizado al compresor, localizado en el estado termodinámico del gas entre el impeller y el difusor. Las trayectorias de eficiencia instantánea, pi y pd, que representan al impulsor y al difusor, conectan este estado con los estados de entrada y salida, al igual que lo hacen en la actual imagen los puntos 0, 1, 2 y 3. El trabajo politrópico, Wpi o Wpd (del impulsor o del difusor respectivamente) es la energía mecánica reversible neta introducida a lo largo de la curva hasta los puntos pi o pd. Las eficiencias de impleller y el difusor, ei y ed, pueden ser definidos por:

• ei = Wpi / ΔHi = Wpi / (Wi - ΔKEi)
• ed = Wpd / ΔHd = Wpi / (Wd - ΔKEd)

Nos referiremos de aquí en adelante a este conjunto de relaciones como (4b).

En las relaciones de (4b) la entrada de trabajo en el eje, Wi, referida al impeller es también la entrada de trabajo en el eje, W, para la etapa entera. La entrada de trabajo en el eje referida al difusor, Wd, es cero. De estaforma (4b) se puede reescribir como:

• ei = Wpi / (W - ΔKEi)
• ed = Wpi / - ΔKEd

Nos referiremos de aquí en adelante a este conjunto de relaciones como (4c).

De la relación anterior (4c) y la relación (4) se deduce también:

• (Wpi / ei) + (Wpd / ed) = Wp / e   (39)

Donde Wp y e son el trabajo de la etapa y la eficiencia. Una ecuación parecida a (39), puede relacionar también el trabajo de la etapa individual y la eficienca con la global del compresor, a continuación veremos cómo. Los coeficientes de trabajo del impeller y el difusor, μi y μd, son definidos a partir de la relación (26) de la siguiente forma:

• μi = (g· Wpi) / ∑ u^2
• μd = (g· Wpd) / ∑ u^2

Nos referiremos de aquí en adelante a este conjunto de relaciones como (26c).

De las relaciones (26), (26c) en conjunto con la (39) tenemos:

• (μi / ei) + (μd / ed) = μ / e   (40)

Donde μ y e son el coeficiente de trabajo de la etapa y la eficiencia. Las ecuaciones (4c), (26c), (39) y (40) se utilizan con nuestras relaciones anteriores para considerar por separado el rendimiento del impulsor y del difusor.

Para terminar, Schultz no lo concreta porque para él puede parece trivial, pero una vez tengamos calculada la velocidad máxima del impller podemos hallar el diámetro de la siguiente forma:

• u = π · D · N

Donde D es el diámetro y N el número de vueltas por unidad de tiempo.

2.7 Presión Total y Temperatura

A lo largo de nuestra entera discusión P y T han representado la presión y temperartura como "estáticas" a diferencia de los valores "intactos" o "totales". Para la presión y temperatura total, Pt y Tt, nos referimos a los valores estacionarios resultantes de una desaceleración isentrópica de un flujo de gas. Esta distinción es solo importante en los test de compresores donde v^2 / 2·g es apreciable comparado a Wp, por ejemplo, en el test de difusores o impellers.

La dificultad  es que un dispositvo sensible a la temperatura en una corriente de gas (un sensor de temperatura), detecte Tt en lugar de T y registre algunas temperaturas intermedias dependiendo de sus características particulares. Asumiendo que esas características son conocidas nosotros podemos superar el problema instalando una sonda de presión para medir Pt. Entonces para combinar (4), (5c), (6i) y (6n) con e = 1, podemos escribir:

•  v^2 / 2·g ~ (Z·R·T / ms) · [(Pt / P)^ms - 1] = Cp·(Tt - T) / (1 + X)
• Tt / T = (Pt / P)^ms
• ms = (Z·R / Cp) · (1 + X) = [(k - 1) / k] · Y / (1 + X)

Nos referiremos de aquí en adelante a este conjunto de relaciones como (41).

Para pequeñas relaciones de Pt / P, la relación (41) puede simplificarse como:

• v^2 / 2·g ≈ (Pt - P)·V
• (Tt - T) / T = ms · [(Pt - P) / P]

Nos referiremos de aquí en adelante a este conjunto de relaciones como (41a).

2.8 Flujo Lateral y refrigeración

Hasta ahora ninguno de los anteriores análisis ha incluido compresores teniendo en cuenta flujo lateral ni refrigeración. El tratamiento del flujo lateral requiere que el compresor sea dividido en unidades de flujo másico constante, teniendo debidamente en cuenta los efectos de la mezcla cuando el flujo lateral es hacia dentro. La homogeneidad de dicha mezcla al entrar en la siguiente etapa puede ser cuestionable, pero normalmente se da por sentada a efectos prácticos.
Se emplea un procedimiento similar para el enfriamiento entre etapas, ya que el compresor se puede subdividir en unidades sin enfriar y las enfriadas entre etapas se tratan por separado. La mayoría de los casos de enfriamiento por inyección de líquido se pueden tratar de esta manera. Incluso el enfriamiento del diagrama se puede manejar de esta manera si la mayor parte del enfriamiento tiene lugar entre la salida del difusor y la entrada de la etapa siguiente.
Si se testea un compresor refrigerado para obtener los valores globales de e y μ, estos solo son significativos para la relación probada entre la refrigeración del gas y la energía mecánica introducida. Tanto la magnitud de esta relación como su distribución dentro del compresor son factores determinantes.

2.9 Otras Aplicaciones

Como cierre conceptual a todo el análisis de diseño tratado en esta publicación de Schultz, podemos decir que el análisis politrópico no está limitado a compresores centrífigos solamente, si no que puede ser aplicado a cualquier máquina compresora de gas. Esto incluye tanto turbinas como compresores, teniendo en cuenta la sustitución de e por la debida eficiencia de la turbina. Donde:

• En el caso de una turbina: tenemos que el gas es quien entrega energía → Baja la H del gas. 
• En el caso de un comrpesor: tenemos que el gas es quien recibe energía → Aumenta la H del gas.

Todo el análisis realizado por Schultz, no está limitado exclusivamente a máquinas, sino que es una teoría general de procesos de gas real. El análisis politrópico es un lenguaje que permite describir cómo varía P, V y T en gases reales, ya sea en una máquina o no. Como por ejemplo en el caso de restricciones cortas y bruscas en líneas (orificios o estrangulamientos como una válvula de expansión, un restrictor fijo en líneas de gas, etc ...), o elementos de aceleración de gas tipo estrechamiento (boquilla o nozzle como la tobera de una turbina, la boquilla de un quemador, etc ...).

La determinación de orificios y caudal de la boquilla pueden ser calculados por las relaciones (4) o (29) usando e = es = 1, con (5b) o (5c), (6i), (6n) y un coeficiente de caudal empírico. ¿Por qué decimos e = es = 1? no hay eje y por tanto no hay eficiencia mecánica. Los resultados son similares a la relación (41), con la adición de una aproximación del factor de velocidad y coeficiente de flujo.

Otra aplicación es la relación P, V y T de un proceso de estrangulamiento, el cual es representado por la relación (6j) y (6n). La relación de la P, V y T de procesos a volumen constante y procesos a temperatura constantes son representados por las relaciones (6n) y (24) o (25). Ojo, estas relaciones no modelan una válvula de expansión u orificio como tal, solo descibe como varían las variables descritas, pero para un diseño de este tipo de dispositivos ya se precisaría coeficiente de descarga, modelo de pérdidas ...

A primera vista un proceso a presión constante parece ser indeterminado por las relaciones (6k) y (6n), la función de proceso politrópico parece fallar. Sin embargo, podemos reformular la relación (6h) adicionándole (6k) con el siguiente resultado a partir de la definición termodinámica de X:

• - (1 / mp·np) = 1 + X   (6u)

Y con la relación anterior reescribimos una de las relaciones de (6n):

• (V / V0)p = (T / T0)p^(1+X)   (6v)

Donde con P denotamos proceso a presión constante.

Para todo lo anterior es importante recalcar que la ecuaciones descritas no modelan dispositivos, modelan procesos. Los dispositivos se obtienen combinando procesos, por ejemplo: un estrangulamiento como un orificio, es un proceso que sufre una caida de presión sin trabajo, y lo podemos combinas con un proceso con apenas cambio de entalpía → podemos combinas las relaciones (6j) y (6n) que tenían esta forma ...

• 6j,
  • para m → mH = (Z·R / Cp) · X = [(k - 1) / k] · [(X · Y )/ (1 + X)^2], donde dnotamos con H para mH un proceso con entalpía constante.
  • para n → nH = 1 / [Y - mH · (1 + X)] = (1 + X) / [Y · (1+(X/k))]
• 6n,
  • (T / T0) = (P / P0)^m = (Z0 / Z)·(P / P0)^[(n-1)/n]
  • (V0 / V) = (P / P0)^(1/n) = (Z0 / Z)·(P / P0)^(1 - m)
  • (P / P0) = (T / T0)^(1/m) = (V0 / V)^n 

2.10 Funciones de Compresibilidad Generalizada

Esta sección tiene un gran contexto para el momento de su publicación en 1962, cuando la información disponible estaba recogida en gráficas. Por esta razón Schultz usa esta sección para explicar como obtener X e Y de gráficas que usan derivadas aproximadas. Hoy en día con la ayuda de software termodinámico (como CoolProp) podemos conocer estas variables para gases reales de forma mucho más directa. 

En conexión con la relación (33), anteriormente se ha mencionado la necesidad de obtener las variables X, Y y Z desde gráficos de compresibilidad generalizada para gasaes en un determinado estado. Muchos de esos gráficos, comenta Schultz, han sido publicados desde 1931 relacionando Z con Pr y Tr. Recordemos que de la ecuación (13), Z puede ser definida como:

• Z = P·V / R·T   (13a)

Mientras que la Presión Reducida y la Temperatura Reducida son definidas como:

• Pr = P / Pc
• Tr = T / Tc

Nos referiremos de aquí en adelante a este conjunto de relaciones como (42).

En la relación (42) Pc y Tc son la Presión Crítica Absoluta y la Temperatura Crítica Absoluta. Se dice que los gases que tienen los mismos valores de Pr y Tr se encuentran en estados similares y, a menudo, tienen casi el mismo valor de Z. El gráfico de Nelson-Obert [bibliografía indicada por Schultz en su artículo], publicado en 1953, correlacionó el valor de Z de 26 diferentes gases dentro de un margen del 2,5% para los límites de 0 ≤ Pr ≤ 10 y 0,6 ≤ Tr ≤ 15, excepto cerca de Pr = Tr = 1. Esos gases incluyen aire, argón, benzeno, dióxido de carbono, etano, iso-butano, metano, neón, oxígeno, nitrógeno, propano y propileno. Sin embargo, fue también publicado que para los gases de amoníaco, helio, hidrógeno, fluoruro de metilo y vapor las correlaciones entre estos son menos precisas. Por lo que Pr y Tr, no se puede decir que sean parámertos de compresibilidad universales. Algunas veces los mejores resultados son obtenidos si se emplean seudovalores de Pc y Tc en las relaciones de (42). Nelson y Obert encontraron que este era el caso del helio y el hidrógeno.Del párrafo anterior tenemos que quedarnos con que dos gases con el mismo Pr y Tr se comportan parecido, y por ello se puede usar una misma gráfica de Z para muchos gases (teniendo en cuenta el error expuesto y en qué gases hay mayores desvíos). El gráfico de Nelson-Obert citado es un gráfico con un eje horizontal para Pr, un eje vertica para Z y cruvas para Tr constantes. 

Para gases cuyos valores de Z pueden ser correlacionados de forma precisa mediante Pr y Tr, usando valores reales o seudovalores de Pc y Tc, es en estos casos también posible correlacionar X e Y. A partir de la relación (42) podríamos escribir la relación (22) de la siguiente forma:

• X = (Tr / Z) · (∂Z/∂T)Pr
• Y = 1 - (Pr / Z) · (∂Z/∂Pr)Tr

Nos referiremos de aquí en adelante a este conjunto de relaciones como (22a).

Entonces desde la relación (22a) se determina X e Y desde la pendiente de las líneas constantes de Pr y Tr, que representan Z. El habitual diagrama de Z contiene líneas de las contantes Tr versus Pr desde las cuales Y puede ser determinada directamente. Un diagrama cruzado para obtener las líneas de las contantes Pr versus Tr es necesario para determinar X.

De esta manera X e Y fueron obtenidas desde el gráfico de Nelson-Obert a través de las regiones de 0 ≤ Pr ≤ 10 y 0,6 ≤ Tr ≤ 15. Esos cálculos gráficos fueron impresos en un diagrama con valores calculados por diferencias finitas sobre las relaciones de (22) para un gas refrigerante común, diclorodifluorometano (refrigerante-12) [extraído de una fuente bibliográfica indicada por Schultz en su publicación], el cual reproduce el gráfico de Nelson-Obert dentro del 3%. Los diagramas preliminares fueron verificados y ajustados por un segundo conjunto de cálculos, para los cuales se emplearon las relaciones de (15c) para el refrigerante-12.

El resultado general de las gráficas de X e Y es mostrado en en la figura 2 y 3. Una revisión de estos gráficos determina la posibilidad de largas desviaciones desde los valores de un gas ideal con X = 0 e Y = 0. Para presiones y temperaturas fuera de la región graficada X puede llegar a ser negativa. Puedes ir a las figuras 2 y 3 al final de este artículo para ver estos diagramas de Nelson-Obert, donde para manejarlos debes tener en cuenta:

• Entrar por un valor Pr y cortar con su vertical la curva constante del valor de Tr en el punto concreto.
• Tomar nota del valor horizontal que corta el punto para hallar el valor Y o de Z, en función de la gráfica que usemos.

Como comenta Schultz estos gráficos fueron construidos a partir de cálculos a mano de la época mediante "diferencias finitas". Esta es una forma común de resolver una derivada de forma aproximada:

• Si tenemos la derivada (∂Z/∂T) para resolverla tenemos que pensar que alfinal es el cálculo de una pendiente pero de infinitesimal (en un paso muy pequeño)
  • (∂Z/∂T) ≈ ( Z(T2) - Z(T1) ) / (T2 - T1)

Mediante software hoy en día, podemos implementar métodos numéricos para hacer estas diferencias finitas, de forma que mediante varias iteraciones obtengamos valores muy precisos.

2.11 Ejemplo Numérico

Schultz cierra su publicación sugiriendo la resolución de un caso práctico, para un proceso de compresión involucrando un gas real. Imaginemos entonces que disponemos de los datos del test real de un compresor centrífugo, con las mismas etapas que nuestra curva p y S0, para el gas Refrigerante-12 con los siguientes datos:

• P0 = 10 psia; T0 = -10 F; P3 = 130 psia; T3 = 210 F

En primer lugar, de una tabla de propiedades termodinámicas [tabla de consulta de Schultz de la que indica su fuente bibliográfica] podemos encontrar los valores para los puntos 0 y 3 siendo conocidas las presiones y temperaturas:

• V0 = 3,8861 ft3/lb; H0 = 76,880 Btu/lb; V3 = 0,41676 ft3/lb; H3 = 106,520 Btu/lb; V4 = 0,37297 ft3/lb; H4 = 97,839 Btu/lb

En segundo lugar, podemos hacer el primer cálculo para conocer los resultados de las relaciones de (27a):

• n = 1,1488; ns = 1,0944; f = 1,015; Wp = 17,285 ft-lb/lb; e = 0,749

La desviación de f respecto a 1,0 muestra que ns varía a lo largo de S0. Schultz señala que esta variación puede ser percibida en la tabla 1, con la relación de los datos tabulados de ns y las propiedades relacionadas a lo largo de S0. También podemos tabular esas propiedades a lo largo de la curva p, sustituyendo n por ns cn e = 0,749. Además de los puntos finales, nuestra tabla debería incluir los puntos medios aproximados de S0 y p, donde Ws y Wp son aproximadamente la mitad de sus totales finales. Los resultados están visibles en la tabla 1.

La tabla 1 muestra una variación en ns a lo largo de S0 del 7,5%, por lo tanto, no es de extrañar que el Ws calculado a partir de una media constante de ns = 1,0944 tenga un error del 1,5 %. La variación de n a lo largo de la curva p es de 6,9%. La similitud de esto respecto a ns, refuerza la decisión de ajustar Wp para f = 1,015 calculado a partir de la relación de ns y Ws. 

La tabla 1 también muestra una desviación apreciable de ns respecto del valor k de un gas ideal. Donde si usamos un valor medio contante de k = 1,173 para predecir el valor de Ws, V4 y ΔTs para las relaciones de gas ideal de (6l) en (5a) y (6n), esto daría 7%, 17% y 22% respectivamente.

Mediante el uso de las ecuaciones gas real en (6i), (5b) y (6n) con un valor medio constante de X = 0,265, Y = 1,076 y f = 1,015, el error correspondiente sería de 0,5%, 1% y 0,5% respectivamente.

Tabla 1 - Curva S0

	Entrada	Medio	Salida
P (psia)	10	39	130
V (ft3 / lb)	3,8861	1,1460	0,37297
T (deg F)	-10	74,11	159,96
H (Btu / lb)	76,880	87,419	97,839
S (Btu /lb deg R)	0,18171	0,18171	0,18171
Cp (Btu / lb deg R)	0,13603	0,15343	0,17462
Cv (Btu / lb deg R)	0,11716	0,13160	0,14558
k	1,1611	1,1659	1,1995
X	0,101	0,220	0,519
Y	1,038	1,057	1,152
Z	0,974	0,943	0,882
ms	0,131	0,123	0,126
ns	1,119	1,103	1,041

 

Tabla 1 - Cruva p

	Entrada	Medio	Salida
P (psia)	10	40	130
V (ft3 / lb)	3,8861	1,1862	0,41676
T (deg F)	-10	102	210
H (Btu / lb)	76,880	91,678	106,520
S (Btu /lb deg R)	0,18171	0,18909	0.19518
Cp (Btu / lb deg R)	0,13603	0,15518	0,17294
Cv (Btu / lb deg R)	0,11716	0,13436	0,14806
k	1,1611	1,1550	1,1680
X	0,101	0,187	0,355
Y	1,038	1,056	1,106
Z	0,974	0,952	0,912
ms	-	-	-
ns	-	-	-
m	0,171	0,153	0,146
n	1,177	1,143	1,101

 

Los valores medios anteriores de k, X e Y fueron estimados por promedios numéricos con doble ponderación dada la mitad, lo que para k sería:

• k = (1,1611 + 2 · 1,1659 + 1,1995) / 4 → k = 1,173

La precisión de estos resultados podrían ser mejorados ligeramente mediante el refinamiento de estos valores medios constantes, pero una precisión perfecta es imposible desde (6m) y no puede reproducirse a (8) de forma perfecta.

Ahora imaginemos que fuera necesario diseñar un compresor centrífugo para la aplicación que se ha discutido, pero sin disponer de información de sus datos termodinámicos a partir de un test. Suponiendo entonces como única información:

• P0 = 10 psia; V0 = 3,8861 ft3/lb; T0 = -10 F; P3 = 130 psia; k = 1,160; R = 12,779 ft-lb/lb deg R;

Pc = 596,9 psia; Tc = 233,6 F, e = 0,749

La solución de este problema requiere que hagamos una asunción de T3, ya que es una incóginta, y verificarla posteriormente mediante la relación (33). Para resumir todo este bloque iteravo hasta que T3 converja, Schultz indica que en este ejemplo aporta el parámetro de T3 ya de forma precisa en la primera iteración para ahorrar pasos iterativos, con T3 = 210 F. Una vez congeturado el valor de T3, tendríamos que calcular los valores medios de X e Y, para lo que necesitamos unos datos tabulados similares a los de la tabla 1, y por lo tanto tendríamos que seleccionar aproximadamente un punto medio de la curva p (curva que en este estado del ejercicio desconocemos). Una elección razonable sería el punto medio logarítmico de la presión ( P0·√[P3/P0] ) y la media aritmética del aumento de temperatura ( T0 + (T3 - T0)/2 ), por ejemplo, P = 36 psia y T = 100 F. ¿Por qué Schultz usa una media logarítmica para la presión y una media aritmética para la temperatura? En las ecuaciones vistas a lo largo de la publicación de Schultz, podemos ver que la mayor parte están formuladas en log(P), estas relaciones describen procesos donde para los casos politrópicos e isentrópicos son casi lineales a escala logarítmica (si los representamos en una gráfica, y el eje de la presión tuviera escala logarítmica apreciaríamos esto). Además de lo anterior, la mayor parte del trabajo termodinámico ocurre a baja presión, por ello es mejor usar la media logarítmica que la presión media, la cual hubiera dado (10 + 130) / 2 = 70 psia y con la media logarítmica tenemos en cambio un valor más bajo, 36 psia. Para terminar con esto, en el caso de la temperatura esta suele variar de forma más lineal, y por ello es acertado usar una media airtmética. 

Los resultados se pueden encontrar en la Tabla 2 con X e Y tomados de las gráficas 2 y 3.

Tabla 2

	Entrada	Medio	Salida
Pr	0,0168	0,0603	0,2178
Tr	0,649	0,807	0,966
X	0,11	0,17	0,36
Y	1,04	1,05	1,10

En la tabla 2 calculamos las medias de X = 0,20 e Y = 1,06. Asumiendo f = 1,000 y aplicando la relación (33) encontramos que:

• m = 0,1559; n = 1,1455; Wp = 16,967; V3 = 0,4141 ft3/lb; T3 = 211,1 F

Comparando estos resultados con los correctos datos de nuestro test real aquí discutido, encontramos errores en Wp, V3 y ΔT del orden de 2%, 1% y 0,5% respectivamente. Si hubieramos usado relaciones de gas ideal los resultados habrían sido:

• m' = 0,1842; n' = 1,2257; Wp = 18,347; V3 = 0,4794 ft3/lb; T3 = 265,5 F

Y en cuanto a los errores de la solución usando relaciones de gas ideal, tenemos 6%, 15% y 23% respectivamente para Wp, V3 y ΔT.

Ahora otro ejemplo, suponiendo que fuera necesario diseñar un compresor para esta misma aplicación, pero con todos los datos termodinámicos disponibles. Usando k = 1,167 y e = 0,749 en la relación (34b) obtendríamos es' = 0,701. Aplicando la relación (35) encontraríamos V3' = 0,41801 ft3/lb y para la relación (27b) e' = 0,744. Entonces tendríamos lo siguente:

• es' / e' = 0,942 y usando la ecuación (34c) obtenemos es = 0,706.

En los datos de la tabla 1, podemos encontrar que el dato correcte es es 0,707.

Alternativamente podríamos haber usado la relación (33c) para encontrar S3 = 0,19502 Btu/lb deg R y T3 = 209,4 F. En la tabla 1 los valores correctos son 0,19518 y 210,0. Esto es solo 0,3 F menos precisa que la anteriormente vista solución isentrópica, y bastante menos complicada.

Para resumir los tres anteriores ejemplos del mismo proceso de compresión, hemos usado tres valores diferentes de k. El primero el valor medio a lo largo de la curva S0, con un valor de 1,173. El segundo, con 1,160, fue el valor medio a lo largo de la curva p. Y el tercero, con 1,167, fue el valor medio entre S0 y p. Cada uno de estos fue el valor más apropiado para cada aplicación en particular. Ningún valor usado de forma única para los tres casos, habría producido una precisión comparable en cada uno de ellos.

3 Conclusiones y Recomendaciones

Schultz nos deja esta última sección en su publicación como broche final.

Las ecuaciones de gas ideal para el análisis politrópico indican, y los ejemplos numéricos realizados comfirman, que la precisión dentro un poco por ciento requiere datos termodinámicos, los cuales existen para algunas aplicaciones. Los ususarios de compresores deben reconocer estas aplicaciones por las cuales están o no espectantes a lo imposible. Además, cuando las tablas termodinámicas o gráficos son preparados, sería más conveniente añadir también Cp o k, X, Y y Z.

Generalmente los datos de compresibilidad son útiles cuando los datos específicos no están disponibles. Desde que las funciones de X e Y han sido definidas  y generalizadas aquí por primera vez, los futuros investigadores podrían ser capaces  de mejorar algunas regiones de la figura 2 y 3. La experiencia podría revelar una necesidad para extenderesas figuras más hallá de Pr = 3 y Tr = 5. Investigaciones para mejorar o extender las figuras 2 y 3 son recomendadas para Schultz en su publicación.

Muchas de las ecuaciones de gas real han sido también derivadas y publicadas en este artículo por primera vez. Futuros reajustes y derivaciones podrían mejorar su ultilidad. En este contexto, una derivada para generalizar el polytropic head factor (factor de trabajo politrópico), f, sería bastante útil.

Para acabar Schultz indica en su artículo que el ASME Power test Code for Centrifugal, Mixed flow, and Axial Compressors and Exhausters (PTC10-1949) debería ser reescrito para incluir el análisis politrópico y test de rendiemiento equivalente. Schultz comenta que el Código de aquel momento está basado en análisis isentrópicos y por lo tanto no puede ser válido para tests equivalentes.

     Figura 2 - Función X de compresibilidad generalizada [John M. Schultz, 1962]

Figura 3 - Función Y de compresibilidad generalizada [John M. Schultz, 1962]

 

Y hasta aquí la explicación de la publicación de Schultz de 1962 en ASME, una publicación que sentó las bases del análisis polotrópico para poder diseñar equipos de compresión para gases reales de forma precisa, y que hoy en día, lejos de los cálculos manuales y gráficos, seguimos implementando en los softwares de procesos más potentes.