En datos del 2023 solo un 1% del H₂ producido es de bajas emisiones ( electrólisis u origen fósil con captura de CO₂). La mayoría del hidrógeno sigue produciéndose a partir de gas natural (~66%) y carbón (~20%), especialmente China, que concentra el 90% del hidrógeno basado en carbón. 🛢️🔥

Otra parte significativa del hidrógeno producido mundialmente proviene como subproducto en refinerías y la industria petroquímica.

Puedes visitar la web de la IEA para ver datos como estos sobre la producción global de H₂. 🌐

 

1. La electrólisis del agua: fundamentos y energía requerida ⚡🔬

H₂O → H₂ + ½ O₂

• H₂O + 2e- → H₂ + O2-
• O2- → ½ O₂ + 2e-

La anterior reacción muestra la electrólisis del agua; aplicándole una tensión eléctrica suficiente podemos lograr dividirla en H₂ y O₂ gracias a esta transferencia de cargas.

La energía necesaria para poder generar esta reacción, en condiciones de 25 ºC y 1 kPa es:

• ΔH° = 285,83 kJ/mol (≈ 39,4 kWh/kg H₂) 🔥

*Nota: este cero encima del delta de entalpía es usado para indicar que se está evaluando en condiciones estándar de Tª y presión.

Lo que es conocido como la entalpía de reacción en condiciones estándar. Esta energía necesaria es calculada como:

• ΔH°r​ = ∑ΔH°f​ (productos) − ∑ΔH°f​ (reactivos), que sustituyendo...
• ΔH°r ​= [ΔH°f (H2(g)) + 0,5​ΔH°f​ (O2(g))] − ΔH°f​ (H2O(l)), sustituyendo con datos de tablas de propiedades químicas...
• ΔH°r ​= [0 + 0,5 x 0] − (-285,83 kJ/mol), lo que expresado en kWh por cada kg de H2 producido...
• 39,4 kWh/kg H₂

Conocer esta energía es la base para saber cuál es la tensión eléctrica necesaria a inducir al agua, y cuál es la intensidad de corriente necesaria para producir tanto H₂ como se desee.

Y ahora que sabemos cuánta energía necesitamos aplicar al agua para producir H₂, ¿cuánta energía necesitamos aplicar a otras formas de producción de H₂ convencionales?

 

2. Otras rutas industriales para obtener hidrógeno 🏭

2.1. Reformado con vapor de metano (SMR) 🔥

La reacción de reformado de gas natural con vapor consiste en la mezcla de vapor de agua con gas natural, y la aplicación de calor a esta mezcla.

CH₄ + H₂O → CO + 3H₂

El gas natural suele conllevar una desulfuración previa, y una vez obtenido el CO y el H2 se suelen concatenar con otras reacciones como autorreformado, water-gas shift, metanación... Pero para la reacción tratada, en resumen, tenemos la siguiente necesidad de energía:

• ΔH°r ≈ +206 kJ/molCH₄ (endotérmica), lo que expresado en kWh por cada kg de H2 producido...

• Por cada mol de CH₄ tenemos 3 de H₂, lo que hace para un kg de H₂ necesitemos 165,34 mol de CH₄. Esto nos da (164,35 x 206) kJ/kg H₂, y expresado en kWh/kg H₂...

• 9,46 kWh/kg H₂ (sin captura de CO₂), cuatro veces menos energía que la electrólsis del agua.

2.2. Gasificación del carbón 🏭🔥

De la misma forma que la adición de vapor al gas natural puede producir H2, la adición de vapor al carbón en las condiciones de temperatura adecuadas también es capaz de arrancar H2 al agua:

C + H₂O → CO + H₂

Resolviendo la entalpia de reacción en condiciones estándar tenemos:

• ΔH°r ≈ +131 kJ/molC, lo que expresado en kWh por cada kg de H₂ producido...

• 18,11 kWh por cada kg de H₂, dos veces menos energía que la electrólisis del agua.

 

Puedes encontrar más información sobre los usos industriales del hidrógeno en este artículo. 📚

3. La energía de la electrólisis explicada desde la termodinámica 🔍

3.1. Entalpía de reacción estándar del agua

Como hemos visto anteriormente, para ejecutar la reacción de división del agua precisamos inyectar una energía determinada. Pero esta energía necesaria es un cómputo entre electrones y calor, es decir, aplicar un voltaje suficiente para garantizar el transporte de electrones y, además, la aplicación de calor al agua.

• ΔH° = 285,83 kJ/mol (39,4 kWh/kg)

Para evaluar cuánta parte de esta energía debe darse en forma eléctrica y cuánta en forma de calor, dividimos la entalpía de la reacción en estas dos componentes: calor como TΔS, y trabajo eléctrico como ΔG.

3.2. La ecuación de la Energía Libre de Gibbs y sus implicaciones

Esta ecuación relaciona la entalpía de reacción, o energía total necesaria para la electrólisis del agua, con la cantidad de aporte en trabajo eléctrico y de calor de la siguiente forma:

• ΔG = ΔH – TΔS

La energía libre de Gibbs (ΔG) es una medida del trabajo útil, trabajo necesario para crear un sistema a temperatura y presión constantes, restándole el aporte de calor que el entorno le pudo haber dado. En el contexto de la electrólisis del agua, representa la cantidad mínima de trabajo eléctrico que debe suministrarse para que la reacción (no espontánea) ocurra, sin contar el calor de aporte necesario.

La entropía (ΔS) mide el grado de desorden o dispersión de la energía en una reacción; cuanto mayor es la entropía de un sistema, más cantidad de microestados son posibles. En la electrólisis del agua, el sistema pasa de una molécula líquida (agua) a dos gases (hidrógeno y oxígeno), lo que aumenta considerablemente el desorden. Ese aumento de entropía hace que parte de la energía necesaria para romper la molécula de agua pueda ser absorbida como calor del entorno, en lugar de electricidad.

A partir de esta relación, ya podemos calcular cuánta energía en forma de electricidad necesitaremos (voltaje y carga eléctrica) y cuánta en forma de calor.
Te dejo un ejemplo de cómo hallar estos parámetros en condiciones estándar (a 25 ºC y 1 kPa):

• Primero necesitamos disponer de los siguientes datos: 

Componente	ΔH°f​ (kJ/mol)	S° (J/mol K)
H₂O (l)	-285,83	69,91
H₂ (g)	0	130,68
O₂ (g)	0	205,15

Estos datos son propiedades químicas disponibles en tablas de cualquier bibliografía química.

Nota: no olvides que estos datos tabulados son entropías y entalpías de formación estandar de cada una de las sustancias. No debes confundir estos valores con los calculados en softwares de propiedades termodinámicas como este, como te digo, estos datos son propiedades químicas.

• Segundo, para evaluar ΔG°, no tenemos más que aplicar la ecuación de Gibbs: ΔG° = ΔH° – TΔS°
• Lo que sería obtener ΔH°r = 285,83 kJ/molH₂ y ...
•  ΔS°r = ∑ΔS° (productos) − ∑ΔS°​ (reactivos) = (130,68 + 0,5 x 205,15) - (69,91) = 163,35 J/molH₂K

Nota: recordar la estequimetría de la reacción: 1 mol H2O, 1 mol H2 y 0,5 mol O2

• Total, tenemos ΔG° = ΔH° – TΔS° => ΔG° = 285,83 kJ/molH₂ - 298,15K x 163,35 J/molH₂K = 237,13 kJ/molH₂

Para el ejemplo anterior, tenemos que para generar un mol de H₂ bajo la reacción de electrólisis del agua, necesitamos:

• 237,13 kJ/molH₂ en forma de trabajo eléctrico. ⚡
• T · ΔS°r = (298,15 K) · (163,35 J/molH₂·K) = 48,70 kJ/molH₂, en forma de energía térmica o calor. 🔥

Todo lo anterior, recordemos, para condiciones estándar de temperatura y presión. Ahora pasaremos a ver como relacionar esto con el voltaje eléctrico necesario para generar la reacción.

 

4. Cómo se calcula el potencial eléctrico necesario: Vtn y Vrev ⚡🔋

Hemos visto como hallar la energía necesaria para dar lugar a la reacción. Y tras ello, como conocer cuanta debe aportarse en forma eléctrica, y cuanta en forma de calor. Pero, ¿qué potencial eléctrico debo suministrar al agua como mínimo para que se de la reacción? Para esto tenemos las siguientes relaciones:

• Welec = G, el trabajo eléctrico (mover carga eléctrica de un punto a otro) es igual a la energía libre de Gibbs.
• Welec = E · Q, trabajo eléctrico o energía eléctrica, es igual al potencial eléctrico por la carga (tensión por corriente de toda la vida).
• Depejando... G = E · Q, donde Q es igual a (n · F), el número de moles de electrónes por mol de H₂ multiplicado por la constante de Faraday (carga eléctrica en un mol de electrónes).

Nota: recordar que para la formación de un mol de H₂ necesitamos, dos moles de electrones, por esto, n será igual a 2.

• Finalmente tenemos: E = G / (n · F), potencial eléctrico mínimo para que se de la reacción.

4.1. Potencial reversible y potencial termoneutro de la electrólisis

Hemos visto como relacionar la energía eléctrica necesaria con el potencial eléctrico, con una operación muy simple. Pero, ¿que pasa si también dividimos la entalpía entre n·F, o la energía en forma de calor T·ΔS?

Con estas cuestiones tenemos dos conceptos muy importantes en la electrólisis: potencial reversible y potencial termoneutro.

• Potencial reversible → Vrev = ΔGº/nF => {para nuestro ejemplo en condiciones estandar} => 

=> Vrev = (237,13 kJ/molH₂) / (2 x 96.485 C/molH₂) = 1,23 V (a 25ºC y 1 kPa)

Donde n sería el número de moles de electrones necesarios para 1 mol de H₂ (acorde a la reacción), y F es la constante de Faraday (96.485 C/mol). Este potencial eléctrico sería idealmente el necesario para que la fuerza electrostática entre las celdas pueda generar esta transferencia de electrones. Idealmente entonces, a esta tensión eléctrica, la producción de H₂ será proporcional a la corriente (electrones por unidad de tiempo).

Si hicieramos operar la reacción en sentido contrario (O2 + H2), esta sería la tensión eléctrica que podríamos generar (operación en modo pila), por ello es "reversible".

Pero a la reacción además de darle esta tensión, hemos dicho que necesitamos darle un aporte de calor.

• Potencial termoneutro → Vtn = ΔHº/nF => {para nuestro ejemplo en condiciones estandar} => 

=> Vtn = (285,83 kJ/molH₂) / (2 x 96.485 C/molH₂) = 1,48 V (a 25ºC y 1 kPa)

En esta expresión estamos usando la energía total de reacción, la entalpía, y con ella estamos evaluando la tensión eléctrica nenecesaria para dos cosas conjuntamente:

• Primero: generar la tensión suficiente para crear transferencia de cargas, lo que anteriormente hemos identificado como potencial reversible.
• Segundo: darle el aporte suficiente en forma de calor a la reacción.

Es decir, que la diferencia entre Vtn y Vrev (1,48 - 1,23 = 0,25 V) es una tensión eléctrica que provocará una fuerza electrostática a las cargas superior a la necesaria, y esto producirá unas pérdidas en calor tan grandes como la reacción necesita para tener lugar. En este voltaje termoneutro por tanto, la reacción se autosostiene con solo aporte eléctrico, porque se genera su propio calor.

Si quisieramos conocer la tensión eléctrica adicional para producir calor, podríamos expresarlo también como:

• V = TΔS/nF

Hay que tener en cuenta, que las anteriores tensiones eléctricas son ideales, en la reacción se producen sobre potenciales eléctricos indeseados por diferentes factores (sobrepotenciales por activación, por resistencias ohmicas, transferencias de masa...), lo que da lugar a que en la realidad el rendimiento de esta reacción no pueda llegar al 100%, y que cuanta más corriente se maneje, mayor sea este sobrepotencial.

4.2. Cálculo de la energía eléctrica necesaria para 1 kg de H₂, usando la constante de Faraday

Acorde a lo que hemos visto anteriormente, si queremos producir un kg de H₂ podemos inducir (idealmente) una tensión termoneutra de 1,48 V, y con esto podremos producir tanto H₂ como cargas eléctricas tengamos. Lo que para un kg de H₂ sería:

• 1 mol H₂ = 2,016 g → 1 kgH₂ = 496 molH₂

• Para producir 1 mol de H₂ necesitamos 2 mol de e-.

• Carga, Q = n·F = (2 mol e- / mol H₂) · (496 mol H₂)  · F = 2 · 496 · 96485 = ~95,8·10⁶ C

• Energía eléctrica = V · Q = 1,48 V · 95,8·10⁶ C = 141,78 MJ => {3,6 MJ = 1 kWh} => 39,38 kWh

Esto, a 25ºC y 1 kPa, nos da la energía necesaria para producir 1 kgH₂. Que precisamente es muy similar al poder calorífico superior del H₂: la máxima energía que podríamos obtener de quemar 1 kgH₂, aprovechando hasta la energía del vapor de agua generado en la reacción.

Cuando un fabricante de electrólisis nos da un consumo específico de energía, por ejemplo 54 kWh/kgH₂, no tenemos más que compararlo con la energía teórica que precisamos:

• 39,38 kWh / 54 kWh = 72,93% de rendimiento respecto a su máximo teórico termoneutro.

Y, ¿qué pasa si usamos en este cálculo la tensión reversible?

• Energía eléctrica = V · Q = 1,23 V · 95,8·10⁶ C = 117,47 MJ => {3,6 MJ = 1 kWh} => 32,63 kWh

Este resultado es muy similar al poder calorífico inferior del H₂, es decir, el calor que desprendería quemar 1 kgH₂, pero esta vez sin aprovechar el calor del agua formada en la reacción en estado vapor. Para el ejemplo anterior de consumo específico de 54 kWh/kgH₂, ahora tendríamos:

• 32,63 kWh / 54 kWh = 60,43% de rendimiento respecto a su máximo teórico reversible.

 

6. El efecto de la temperatura: ventajas de la electrólisis de alta Temperatura 🌡️⚡

Hasta ahora hemos evaluado los potenciales eléctricos de la reacción en condiciones estándar pero, ¿qué pasa si aumentamos la temperatura de la reacción?

Pues para esto necesitamos evaluar como varían ΔH y ΔS con la temperatura. de forma aporximada para unos cálculos rápidos podemos aproximarlos así:

• ΔH (T) ≈ ΔHº → podríamos asumirla constante, con lo que Vtn (T) = Vºtn, sería constante a ~1,48 V.
• ΔS (T) ≈ ΔSº → podríamos asumirla constante también, pero recordemos como hallábamos Vrev:
  • Vºrev = ΔGº/nF = TΔSº/nF, aunque ΔS (T) la idealicemos constante la temperatura sigue multiplicando, la expresión correcta para tener una buena aproximación sería:

Vrev (T) = Vºrev - (ΔSº/nF)·(T-Tº) → Como puedes observar el voltage decrece con la Tª.

Esto es una de los fenómenos que da una de las mayores oportunidades a la reacción de la electrólsis del agua, conforme aumentamos temperatura de la reacción, la energía que necesitamos aportar es la misma, pero cada vez podemos aportarle menor cantidad de energía en forma de electricidad y más en forma de calor.

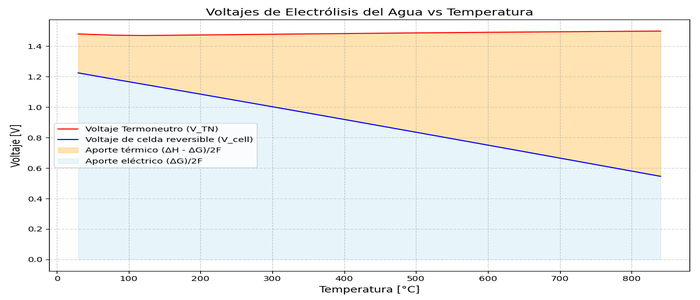
Y esto es posible gracias a la caída del potencial reversible con el aumento de la temperatura. Entender el diagrama Vtn y Vrev con el aumento de la temperatura, y su relación con los voltajes teóricos de la reacción, da una foto muy completa de la termodinámica de la electrólisis del agua. Observa el diagrama de la cabecera de este artículo y guardala en tu memoria.

Hagámos un ejemplo con estas reglas de aproximación para una reacción a 800ºC:

• Vtn (800ºC y 1kPa), como hemos visto anteriormente necesitamos evaluar

ΔHr (800ºC) = ΔH° = 285,83 kJ/molH₂

Vtn = ΔHº / 2F = 285.830 / (2 x 96.485) = 1,447 V

• Vrev (800ºC y 1 atm), para lo que hemos visto

ΔSr (800ºC) = ΔS° = 163,35 J/molH₂K

En esta aproximación, recordemos que NO podemos usar Vrev = ΔG / 2F, donde ΔG era ΔH - TΔS. Usaremos entonces:

Vrev (T) = Vºrev - (ΔSº/nF)·(T-Tº) = 1,23 V - (163,35 / 2·96.485) · (800 - 25) = 0,57 V

6.1. Qué hace única a la electrólisis de alta temperatura, como es el SOEC 🔥⚙️

Como hemos visto para el ejemplo a 800ºC tenemos un voltaje eléctrico teórico de 0,57 V, con un salto hasta el voltaje termoneutro de 0,91 V, esto es una diferencia del 161% respecto al voltaje reversible.

¿Qué pasa en la electrólisis de baja temperatura?

• Vºtn = 1,48 V
• Vºrev = 1,23 V
• 20% respecto al voltaje reversible.

Y este 20% es superado con creces por los sobrepotenciales que se dan en la realidad, con lo que un electrolizador de baja temperatura (menor a 100ºC de operación), está operando por encima del voltaje termoneutro, y por tanto disipando calor. Una reacción exotérmica, en la que nos tenemos que preocupar de ayudar a la reacción a quitarle calor.

En cambio en la electrólisis de alta temperatura el sobrevoltaje sobre el potencial reversible no alcanca el voltaje termoneutro, y la reacción es endotérmica, necesita que le demos calor externo. Aún así la reacción tendrá ineficiencias, pero podemos pagarle en calor (más barato) y no electricidad, y no invertir esfuerzos en retirarle calor.

6.2. Para los más frikis, cómo calcular la variación exacta con la variación de la temperatura. Ley de Kirchhoff

La ley de kirchhoff nos permite evaluar la variación de entalpía y entropía, con la variación de la Tª a presión constante. Veamos el caso de la entalpía:

• ΔH (T2) = ΔH (T1) + ∫ ΔCp (T) dT

Donde Cp se puede evaluar como: Cp = a + bT + cT^2. Podemos integrar esto analíticamente, o podemos hacer una integración trapezoidal de un vector de puntos desde T1 hasta T2, lo que sería aplicar métodos numéricos. Esto es especialmente provechoso si no tenemos una base de datos con coeficientes de polinomios para cada sustancia, como sería un software de pago tipo HYSYS, ya que con Coolprop podemos calcular cada punto y aplicar métodos numéricos.

Lo mismo para el caso de la variación de la entropía con la Tª a presión constante:

• ΔH (T2) = ΔH (T1) + ∫ (ΔCp (T) / T) dT

¿Hay mucha diferencia al aplicar la aproximación que hemos visto anteriormente, respecto a la aplicación de la ley de Kirchhoff? Realmente muy poca. En la imágen de portada se tiene en cuenta la ley de Kirchhoff, y haciendo un zoom de calidad, se aprecian algunos detalles. Como cierta irregularidad en Vtn y Vrev cuando se rebasa la barrera de los ~100ºC, por el cambio de fase a vapor. Otro detalle del zoom, es que a partir del cambio de fase Vtn deja de disminuir (muy levemente) para empezar a aumentar. Sí, el voltaje termoneutro aumenta con la Tª, pero es un aumento muy despreciable, por eso esta subsección es para los más frikis.

6.3. Hemos hablado de las implicaciones del aumento de la Tª, ¿pero qué pasa con la presión?

La ecuación de Nernst nos relaciona el voltaje reversible con la variación de la temperatura y presión, introduciendo el término de Nernst (Q = (PH2·PO2^0,5) / PH2O):

• E (T,P) = [ (ΔH(T) / n·F) - (ΔS(T) / n·F)] - (R·T / n·F)·Ln[(PH2·PO2^0,5) / PH2O]

Donde el neperiano alberga las presiones parciales de reactivos y productos.

Lo que para electrólisis a baja temperatura, a mayor presión se disminuye el voltaje reversible, evaluando el denominador del neperiano como 1, ya que el agua está en estado líquido. Para electrólisis a alta temperatura, donde el agua está en fase vapor, hay que reevaluar las presiones parciales del neperiano.

7. Tabla comparativa de tecnologías: consumo y rendimiento 📊

Tecnología	Tª de Operación	Voltaje típico	kWh/kgH2	Eficiencia [%]
Alcalina	70–90°C	~1,8 V	~52	~76%
PEM	70–90°C	~1,9 V	~55	~72%
AEM	50–70°C	~1,8 V	~50–53	~75–78%
SOEC	500–800°C	~1–1,3 V	~44–46	~85–90%
SOEC con aprovechamiento de calor externo	500–800°C	~1–1,3 V	~37,5	~105%

 

En conclusión la termodinámica implícita en la reacción de electrólisis del agua nos favorece una vía prometedora, como lo es la integración con fuentes térmicas, a la par que la búsqueda de la disminución de sobrepotenciales con el avance tecnológico en nuevos materiales y catalizadores.

 

🔎 Descubre en este otro artículo cómo el SOEC supera el 100% de eficiencia combinándolo con bombas de calor, sin necesidad de fuentes de calor externas.